
7.设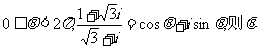 的值为 ( )
的值为 ( )
A.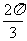 B.
B.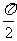 C.
C.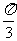 D.
D.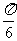
6.某调查者从调查中获知某公司近年来科研费用支出(xi)万元与公司所获得利润(yi)万元的统计资料如下表:
|
序号 |
科研费用支出xi |
利润yi |
xi
yi |
 |
|
1 2 3 4 5 6 |
5 11 4 5 3 2 |
31 40 30 34 25 20 |
155 440 120 170 75 40 |
25 121 16 25 9 4 |
|
合计 |
30 |
180 |
1000 |
200 |
则利润(yi)对科研费用支出(xi)的线性回归方程为 ( )
A.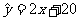 B.
B.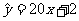 C.
C.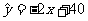 D.
D.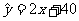
5.侧棱长为4,底面边长为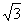 的正三棱柱的各顶点均在同一个球面上,则该球的表面积为
的正三棱柱的各顶点均在同一个球面上,则该球的表面积为
( )
A.76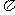 B.68
B.68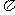 C.20
C.20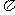 D.9
D.9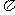
4.若函数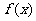 是定义在R上的奇函数,当
是定义在R上的奇函数,当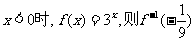 的值是( )
的值是( )
A.-2 B.2 C.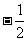 D.
D.
3.若函数 上的函数,则函数
上的函数,则函数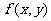 的值域是 ( )
的值域是 ( )
A.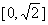 B.
B.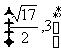 C.
C.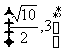 D.
D.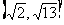
2.已知全集U=R,集合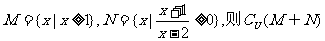 ( )
( )
A.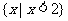 B.
B.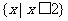
C.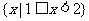 D.
D.
1.函数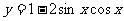 的最小正周期为 ( )
的最小正周期为 ( )
A.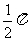 B.
B.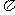 C.2
C.2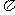 D.4
D.4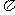
21. (本小题满分14分)
已知椭圆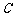 的中心在原点,焦点在
的中心在原点,焦点在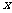 轴上,点
轴上,点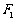 、
、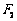 分别是椭圆的左、右焦点,在椭圆
分别是椭圆的左、右焦点,在椭圆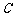 的右准线上的点
的右准线上的点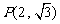 ,满足线段
,满足线段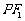 的中垂线过点
的中垂线过点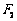 ,直线
,直线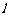 :
: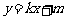 为动直线,且直线
为动直线,且直线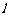 与椭圆
与椭圆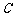 交于不同的两点
交于不同的两点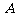 、
、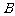 。
。
(Ⅰ)求椭圆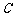 的方程;
的方程;
(Ⅱ)若在椭圆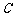 上存在点
上存在点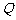 ,满足
,满足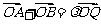 (
(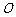 为坐标原点),求实数
为坐标原点),求实数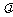 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,当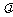 取何值时,
取何值时,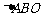 的面积最大,并求出这个最大值.
的面积最大,并求出这个最大值.
20. (本小题满分14分)
已知数列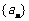 满足
满足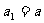 ,
,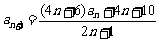 (
(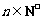 ).
).
(Ⅰ)判断数列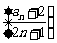 是否为等比数列?若不是,请说明理由;若是,试求出通项
是否为等比数列?若不是,请说明理由;若是,试求出通项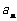 ;
;
(Ⅱ)如果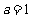 时,数列
时,数列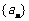 的前
的前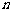 项和为
项和为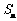 ,试求出
,试求出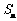 ,并证明当
,并证明当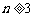 时,有
时,有
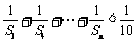 .
.
19. (本小题满分14分)
若存在实常数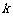 和
和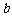 ,使得函数
,使得函数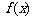 和
和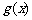 对其定义域上的任意实数
对其定义域上的任意实数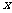 分别满足:
分别满足: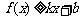 和
和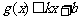 ,则称直线
,则称直线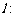
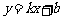 为
为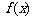 和
和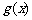 的“隔离直线”.已知
的“隔离直线”.已知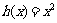 ,
,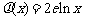 (其中
(其中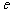 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求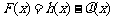 的极值;
的极值;
(Ⅱ) 函数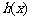 和
和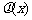 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com