
1.函数 的最小正周期是 ( )
的最小正周期是 ( )
A.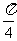 B.
B.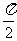 C.
C.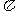 D.
D.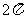
22.(本小题共12分))
设 ,函数
,函数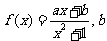 为常数.
为常数.
(1)证明:函数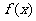 的极大值点和极小值点各有一个;
的极大值点和极小值点各有一个;
(2)若函数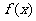 的极大值为1,极小值为-1,试求
的极大值为1,极小值为-1,试求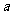 的值.
的值.
21.(本小题共12分)
已知椭圆的方程为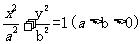 ,过其左焦点
,过其左焦点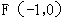 斜率为1的直线交椭圆于P、Q两点,O为原点.
斜率为1的直线交椭圆于P、Q两点,O为原点.
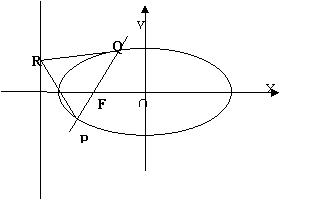

(1)若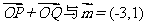 共线,求椭圆的方程;
共线,求椭圆的方程;
(2)若在左准线上存在点R,使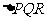 为正三角形, 求椭圆的离心率e的值.
为正三角形, 求椭圆的离心率e的值.
20.(本小题共12分)
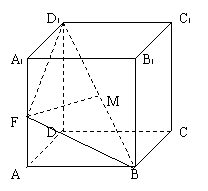
如图:已知棱柱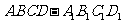 的底面是菱形,且
的底面是菱形,且 面
面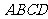 ,
,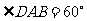 ,
,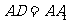 ,
,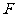 为棱
为棱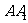 的中点,
的中点,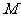 为线段
为线段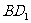 的中点.
的中点.

(Ⅰ)求证:
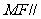 面
面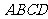 ;
;
(Ⅱ)求证: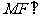 面
面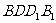 ;
;
(Ⅲ)求面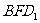 与面
与面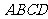 所成二面角的大小.
所成二面角的大小.
19.(本小题共12分)
设数列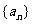 的前n项和为
的前n项和为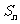 ,且满足
,且满足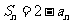 ,n=1,2,3,….
,n=1,2,3,….
(Ⅰ)求数列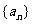 的通项公式;
的通项公式;
(Ⅱ)若数列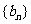 满足
满足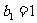 ,且
,且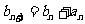 ,求数列
,求数列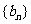 的通项公式.
的通项公式.
18.(本小题共12分)
某学校举办一场以“为希望工程献爱心”为主题的图书义卖活动.同学甲随机地从10本书中买两本,假设每本书被甲同学买走的概率相同.已知这10本书中有3本单价定为10元,4本单价定为15元,3本单价定为20元.记甲同学买这两本书所付金额为ξ(元).求:
(Ⅰ)随机变量ξ的分布列;
(Ⅱ)随机变量ξ的期望Eξ..
17.(本小题共10分)
当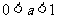 时,解关于
时,解关于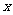 的不等式:
的不等式: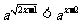
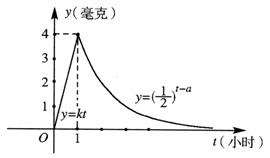
16.某医药研究所开发一种新药,如果成年人按规定的剂量服用,据检测,服药后每毫升血液中的含药量y(毫克)与时间t(小时)之间的关系用如图所示曲线表示.据进一步测定,每毫升血液中含药量不少于0.25毫克时,治疗疾病有效.则服药一次治疗该疾病有效的时间为 小时.
15.4本不同的书全部分给3个同学,每人至少一本,则不同的分法有 种.(数字作答)
14.若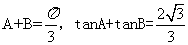 ,则
,则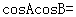 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com