
5.已知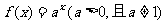 ,
,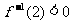 ,则
,则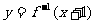 的图像是图中的
的图像是图中的
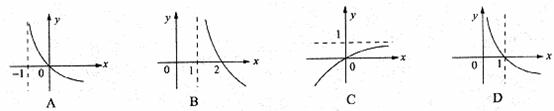
4.函数 在
在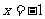 处
处
A.有极大值 B.无极值
C.有极小值 D.无法确定极值情况
3.已知集合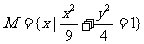 ,
,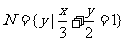 ,则
,则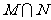 为
为
A.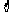 B.
B. 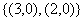
C.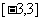 D.
D.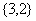
2.“两条直线没有公共点”是“这两条直线异面”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
1.函数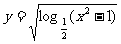 的定义域是
的定义域是
A.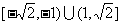 B.
B.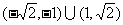
C.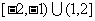 D.
D.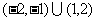
21.(本小题满分14分)长度为 (
( )的线段AB的两个端点A、B分别在
)的线段AB的两个端点A、B分别在 轴和
轴和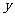 轴上滑动,点P在线段AB上,且满足
轴上滑动,点P在线段AB上,且满足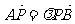 (
(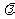 为常数,且
为常数,且 ).
).
(1)求点P的轨迹方程C;
(2)当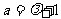 时,过点M(1,0)作两条互相垂直的直线
时,过点M(1,0)作两条互相垂直的直线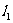 和
和 ,
,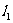 和
和 分别与曲线C相交于点N和Q(N、Q都异于点M),试问△MNQ能不能是等腰三角形?若能,这样的三角形有几个;若不能,请说明理由.
分别与曲线C相交于点N和Q(N、Q都异于点M),试问△MNQ能不能是等腰三角形?若能,这样的三角形有几个;若不能,请说明理由.
20.(本小题满分13分)已知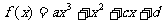 是定义在R上的函数,其图像与
是定义在R上的函数,其图像与 轴的一个交点为(2,0),若
轴的一个交点为(2,0),若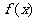 在[-1,0]和[4,5]上是减函数,在[0,2]上是增函数.
在[-1,0]和[4,5]上是减函数,在[0,2]上是增函数.
(1)求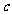 的值;
的值;
(2)求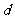 的取值范围;
的取值范围;
(3)若点M在函数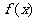 的图像上,且
的图像上,且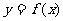 在点M处切线的斜率为-3,求这样的点M的个数.
在点M处切线的斜率为-3,求这样的点M的个数.
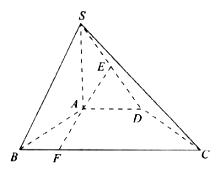
19.(本小题满分12分)如图所示,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC= 90°,SA=AB=AD=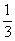 BC=1,E为SD中点.
BC=1,E为SD中点.
(1)若F为底面BC边上一点,且BF=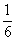 BC,求证:EF//平面SAB;
BC,求证:EF//平面SAB;
(2)底面BC边上是否存在一点G,使得二面角S-DG-B的正切值为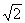 ,若存在,求出G点位置;若不存在,说明理由.
,若存在,求出G点位置;若不存在,说明理由.
18.(本小题满分12分)张先生购买一套没有装修的门面框架房,面积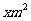 ,购价(成本价) 1000元/m2,办理产权以及杂费1万元,装修费按8000
,购价(成本价) 1000元/m2,办理产权以及杂费1万元,装修费按8000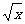 元计算,问:
元计算,问:
(1)一共要多少元钱?
(2)装修后,将此房出租,租金以每年200元/m2计算,5年后此房的成本价不变.①计算5年后由此房所获取利润y与 的函数关系式;②5年后,他计划由此房赚取利润1万元,此房的面积至少为多少?③若他事先花去的所有资金都是从银行以10%的年利率贷款而来(计复利),并计划5年后一次性归还,问他购买100 m2的门面框架房,扣除租金(设租金无息),还需还给银行多少钱?
的函数关系式;②5年后,他计划由此房赚取利润1万元,此房的面积至少为多少?③若他事先花去的所有资金都是从银行以10%的年利率贷款而来(计复利),并计划5年后一次性归还,问他购买100 m2的门面框架房,扣除租金(设租金无息),还需还给银行多少钱?
(注:①y=租金+成本价-购房所需费用与装修费用之和;②当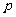 较小时,计算
较小时,计算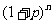 直接用公式
直接用公式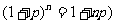
17.(本小题满分12分)在△ABC中,角A、B、C所对的边分别是 、
、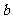 、
、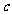 ,tanA=
,tanA=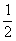 ,cosB=
,cosB=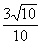
(1)求tanC的值;
(2)若△ABC的最长的边是1,求最短边的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com