
2.等差数列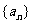 ,已知
,已知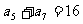 ,
,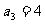 则
则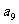 值为
值为
A.8 B.12 C.24 D.25
1.下列集合中,恰有2个元素的集合是
A.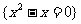 B.
B.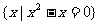
C.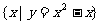 D.
D.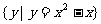
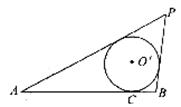
21.(本小题满分l4分)如图所示,已知线段|AB|=4,动圆O’与线段AB切于点C,且|AC|-|BC|=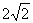 ,过点A、B分别作⊙O’的切线,两切线相交于点P;且P、O’在AB的同侧.
,过点A、B分别作⊙O’的切线,两切线相交于点P;且P、O’在AB的同侧.
(1)建立适当的坐标系,当O’位置变化时,求动点P的轨迹E的方程;
(2)过点B作直线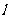 交曲线E于M、N,求△AMN面积的最小值.
交曲线E于M、N,求△AMN面积的最小值.
20.(本小题满分13分)已知,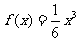 ,
,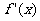 为
为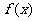 的导数,
的导数,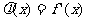 .
.
(1)求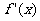 ,
,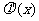 ;
;
(2)若g(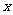 )=
)=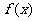 -
-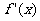 -
-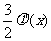 ,求g(
,求g(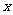 )的单调增区间;
)的单调增区间;
(3)解关于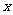 的不等式:
的不等式: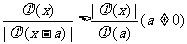 .
.
19.(本小题满分12分)已知数列{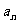 )中,
)中,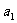 =3,前n项和Sn=
=3,前n项和Sn=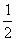 (n+1)(
(n+1)(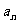 +1)一1.
+1)一1.
(1)求证:数列{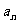 }是等差数列;
}是等差数列;
(2)求数列{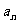 }的通项公式.
}的通项公式.
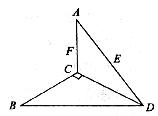
18.(本小题满分12分)如图所示,在ABCD中,∠BCD=90°,BC=CD=1,AC⊥平面BCD,∠ADC=45°,E是线段AD的中点,F是线段AC上的一个动点.
(1)确定点F的位置,使平面ABD⊥平面BEF;
(2)当平面ABD⊥平面BEF时,求直线DB与EF所成的角.
17.(本小题满分12分)某中学高三①、②两班同学进行拔河比赛,①班在每局比赛中获胜的概率都是P.
(1)若比赛5局,①班恰好负2局的概率等于②班恰好胜4局的概率,试求P的值;
(2)若比赛8局,则①班恰好胜4局的概率可能是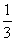 吗?为什么?
吗?为什么?
16.(本小题满分12分)已知△ABC的面积为1,tanB=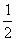 ,tanC=-2,求△ABC的各边长及tanA.
,tanC=-2,求△ABC的各边长及tanA.
15.用砖砌墙,第一层(底层)用去全部砖块的一半多一块,第二层用去剩下的一半多一块,……依此类推,每一层都用去了上一层剩下的砖块的一半多一块,如果到第九层恰好砖块用完,那么一共用了_ __ __块砖.
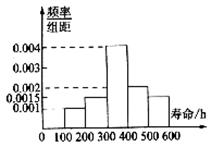
14.某厂研究生产了一种新型电子元件,现随机从中抽取了200个元件进行寿命终极度试验,得到频率分布直方图如图所示.则寿命在100-200h的元件有_______个;估计合格品(寿命在100-400h)的概率为___________;估计总体寿命平均值为__________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com