
4.设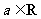 ,且
,且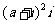 为正实数,则
为正实数,则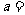
A.2 B.1 C.0 D.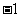
3.在 中,
中,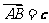 ,
,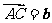 .若点
.若点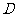 满足
满足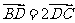 ,则
,则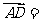
A.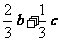 B.
B.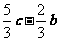 C.
C.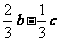 D.
D.
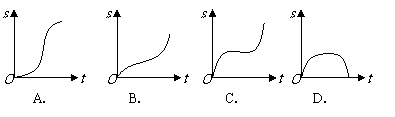
2.汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程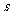 看作时间
看作时间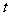 的函数,其图像可能是
的函数,其图像可能是
1.函数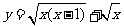 的定义域为
的定义域为
A.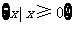 B.
B.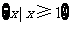
C. D.
D.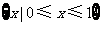
22.(满分14分)抛物线C的方程为 ,过抛物线C上一点P(
,过抛物线C上一点P(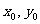 )(
)(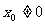 )作斜率为
)作斜率为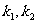 的两条直线交抛物线于A(
的两条直线交抛物线于A(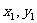 ),B(
),B(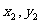 )两点,(P、A、B三点互不相同),且满足
)两点,(P、A、B三点互不相同),且满足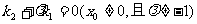 。
。
(1)设直线AB上一点M,满足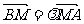 证明线段PM的中点在y轴上。
证明线段PM的中点在y轴上。
(2)当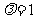 时,若点p的坐标为(1,-1),求∠PAB为钝角时,A的纵坐标y1的取值范围。
时,若点p的坐标为(1,-1),求∠PAB为钝角时,A的纵坐标y1的取值范围。
20.(满分12分)已知函数
(1)若函数 上递增,在区间
上递增,在区间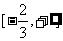 递减,求a的值。
递减,求a的值。
(2)当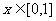 时,设函数
时,设函数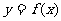 图像上任意一点处的切线的倾斜角为
图像上任意一点处的切线的倾斜角为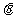 ,若给定常数
,若给定常数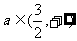 ,求
,求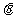 的取值范围。
的取值范围。
|

(1)若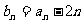 ,求
,求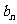 的通项公式;
的通项公式;
(2)若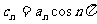 ,求数列
,求数列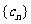 的前n项和pn。
的前n项和pn。
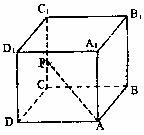
19.(满分12分)如图,边长为1的正方体ABCD-A1B1C1D1,P是CC1上一点,CP=m(0<m<1)。
(1)若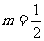 ,求证平面BPD1⊥平面BDD1B1;
,求证平面BPD1⊥平面BDD1B1;
(2)试确定m的值,使直线AP与平面BDD1B1所成的角的正切值为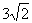 。
。
18.(满分12分)三名短跑运动员,100m成绩合格的概率分别是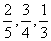 ,如果对这三名运动员的100m成绩进行一次检测,问:
,如果对这三名运动员的100m成绩进行一次检测,问:
(1)三人都合格与三个都不合格的概率是多少?
(2)出现几个人合格的概率最大?
17.(满分12分)已知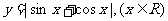
(1)画出函数在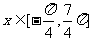 的简图;
的简图;
(2)写出函数的最小正周期和单调增区间,问:当x取何值时函数有最大值,最大值是什么?
(3)若x是△ABC的一个内角,当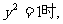 试判断△ABC的形状。
试判断△ABC的形状。
16.设有四个条件:
|
 与平面
与平面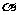 ,
,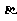 所成的锐二面角相等;
所成的锐二面角相等;
②直线a//b,a⊥平面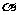 ,b⊥平面
,b⊥平面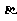 ;
;
③直线a, b是异面直线,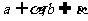 ,且a//
,且a//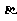 ,b//
,b//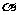 ;
;
④平面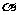 内距离为d的两条平行线在平面
内距离为d的两条平行线在平面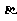 内的射影仍是距离为d的两条平行线。
内的射影仍是距离为d的两条平行线。
其中能推出平面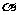 //
//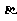 的条件有
(所有正确命题的序号)
的条件有
(所有正确命题的序号)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com