
1.集合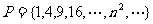 ,若对于运算“*”:“对任意
,若对于运算“*”:“对任意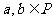 ,都有
,都有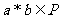 ”,则运算“*”可以是
”,则运算“*”可以是
A.加法 B.减法 C.除法 D.乘法
21.(本小题满分14分)对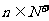 ,不等式组
,不等式组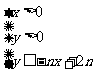 所表示的平面区域为
所表示的平面区域为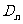 ,把
,把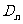 内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:
内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列: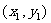 ,
,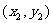 ,
,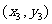 ,…,
,…, 。
。
(1)求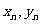 ;
;
(2)若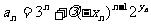 (
( 为非零常数),问是否存在整数
为非零常数),问是否存在整数 ,使得对任意
,使得对任意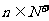 ,
,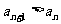 。
。
20.(本小题满分13分)已知点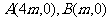 (m是大于0的常数),动点P满足
(m是大于0的常数),动点P满足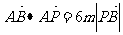 。
。
(1)当点P的轨迹C的方程;
(2)Q是轨迹C上点,过点Q的直线 经过
经过 轴上点
轴上点 ,且交
,且交 轴于点M,若
轴于点M,若 ,求直线
,求直线 的斜率。
的斜率。
19.(本小题满分12分)已知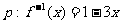 的反函数,且
的反函数,且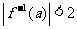 。
。 集合
集合 ,且
,且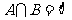 。求实数
。求实数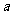 的取值范围,使
的取值范围,使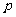 、
、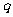 中有且只有一个为真命题。
中有且只有一个为真命题。
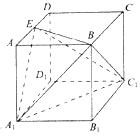
18.(本小题满分12分)如图所示,在边长为1的正方体 中,E为AD的中点。
中,E为AD的中点。
(1)求二面角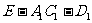 的平面角的余弦值;
的平面角的余弦值;
(2)求四面体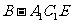 的体积。
的体积。
17.(本小题满分12分)已知:定义域为R的函数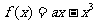 在区间
在区间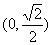 内是增函数。
内是增函数。
(1)求实数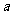 的取值范围;
的取值范围;
(2)若 的极小值为
的极小值为 ,求实数
,求实数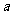 值。
值。
16.(本小题满分12分)设函数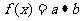 ,其中向量
,其中向量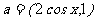 ,
,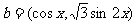 ,
,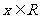 。
。
(1)若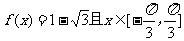 ,求
,求 ;
;
(2)若函数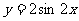 的图像按向量
的图像按向量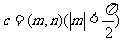 平移后得到函数
平移后得到函数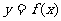 的图像。求数
的图像。求数 、
、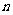 的值。
的值。
15.已知 、
、 是空间两条不同直线,
是空间两条不同直线, 、
、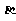 是空间两个不同平面,给出下列四个条件:
是空间两个不同平面,给出下列四个条件:
①平面 、
、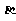 都垂直于平面
都垂直于平面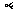 ;
;
②平面 内存在不共线的三点到平面
内存在不共线的三点到平面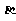 的距离相等;
的距离相等;
③ 、
、 是平面
是平面 内两条直线,且
内两条直线,且 ∥
∥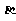 ,
, ∥
∥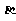 ;
;
④ 、
、 是两条异面直线,且
是两条异面直线,且 ∥
∥ ,
, ∥
∥ ,
, ∥
∥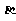 ,
, ∥
∥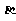 。其中可判断平面
。其中可判断平面 与平面
与平面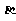 平行的条件是 。(写出所有正确条件的序号)
平行的条件是 。(写出所有正确条件的序号)
14.已知A箱内有红球1个和白球5个,B箱内有白球3个,现随意从A箱中取出3个球放入B箱,充分搅匀后再从中随意取出3个球放入A箱,则红球由A箱移入B箱,再返回到A箱的概率等于 。
13.把容量为100的某个样本数据分为10组,并填写频率分布表,若前七组的频率之和为0.79,而剩下的三组的频数成公比大于2的整数等比数列,则剩下三组中频数最高的一组的频数为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com