
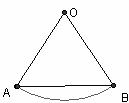
15.如图:在半径为1cm,圆心角为60o 的扇形上,随机撒一把豆子,则落在∆OAB的概率是 .
|
14.已知数列 满足
满足
 且
且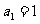 ,则数列
,则数列 的前十项的和是
.
的前十项的和是
.
22.C (本小题满分10分)选修4-5:不等式选讲
已知不等式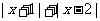
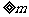 的解集是
的解集是
(1)求实数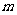 的取值范围:
的取值范围:
(2)在(1)的条件下,当实数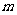 取得最大值时,试判断
取得最大值时,试判断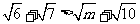 是否成立?并证明你的结论。
是否成立?并证明你的结论。
22.B (本小题满分10分)选修4-2:坐标系与参数方程
(1)已知点C极坐标为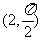 ,求出以C为圆心,半径r=2的圆的极坐标方程
,求出以C为圆心,半径r=2的圆的极坐标方程
(写出解题过程);
(2)把圆C的极坐标方程化成直角坐标方程。
22.A (本小题满分10分)选修4-1:几何证明选讲
如图所示,AB为圆O的直径,BC,CD为 圆O的切线,B,D为切点。
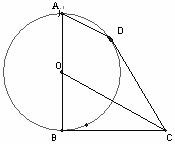
(1)求证:AD∥OC;
(2)若圆O的半径为1,求 的值。
的值。
20.(本小题满分12分) 已知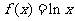 ,
,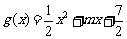 (
(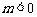 ),直线
),直线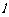 与函数
与函数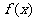 、
、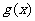 的图像都相切,且与函数
的图像都相切,且与函数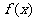 的图像的切点的横坐标为1.
的图像的切点的横坐标为1.
(Ⅰ)求直线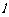 的方程及
的方程及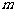 的值;
的值;
(Ⅱ)若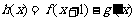 (其中
(其中 是
是 的导函数),求函数
的导函数),求函数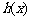 的最大值;
的最大值;
|
|
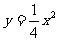 的焦点,离心率等于
的焦点,离心率等于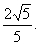
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过椭圆C的右焦点作直线l交椭圆C于A、B两点,交y轴于M点,若
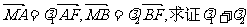 为定值.
为定值.
|
19.(本小题满分12分)如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,AA1=3,D为AC的中点.
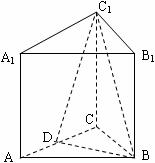
(Ⅰ)求证:AB1 // 面BDC1;
(Ⅱ)求二面角C1-BD-C的余弦值;
(Ⅲ)在侧棱AA1上是否存在点P,使得CP⊥面BDC1?并证明你的结论.
18.(本小题满分12分)一个口袋中装有大小相同的2个白球和4个黑球.
(Ⅰ)采取放回抽样方式,从中摸出两个球,求两球恰好颜色不同的概率;
(Ⅱ)采取不放回抽样方式,从中摸出两个球,求摸得白球的个数的期望和方差.
17.(本小题满分12分)在三角形ABC中, =(cos
=(cos ,sin
,sin ),
), 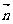 =(cos
=(cos ,-sin
,-sin 且
且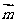 、
、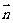 的夹角为
的夹角为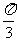
(1)求C;
(2)已知c=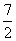 ,三角形的面积S=
,三角形的面积S=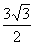 ,求a+b(a、b、c分别∠A、∠B、∠C所对的边)
,求a+b(a、b、c分别∠A、∠B、∠C所对的边)
16.给出下列四个命题:
①命题“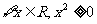 ”的否定是“
”的否定是“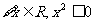 ”;
”;
②线性相关系数r的绝对值越接近于1,表明两个随机变量线性相关性越强;
③若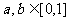 ,则不等式
,则不等式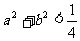 成立的概率是
成立的概率是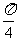 ;
;
④设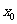 是方程
是方程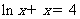 的解,则
的解,则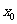 属于区间 (2,3 ).
属于区间 (2,3 ).
其中真命题的序号是 。(填上所有真命题的序号)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com