
(13)若x,y满足约束条件 则z=2x-y的最大值为 .
则z=2x-y的最大值为 .
(14)已知抛物线y=ax2-1的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 .
(15)在△ABC中,∠A=90°,tanB=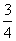 .若以A、B为焦点的椭圆经过点C,则该椭圆的离心率e= .
.若以A、B为焦点的椭圆经过点C,则该椭圆的离心率e= .
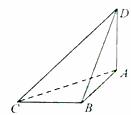
(16)已知菱形ABCD中,AB=2,∠A=120°,沿对角线BD将△ABD折起,使二面角A-BD-C为120°,则点A到△BCD所在平面的距离等于 .
3.本卷共10小题,共90分。
(1)函数y=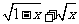 的定义域为
的定义域为
A.{x|x≤1} B. {x|x≥1}
C.{x|x≥1或x≤0} D.{x|0≤x≤1}
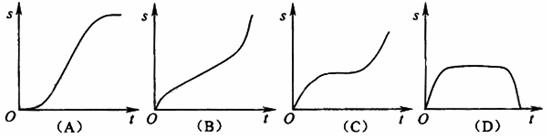
(2)汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程s看作时间t的函数,其图像可能是
(3)(1+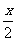 )
)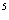 的展开式中x
的展开式中x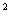 的系数
的系数
A.10 B.5 C.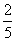 D.1
D.1
(4)曲线y=x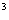 -2x+4在点(1,3)处的切线的倾斜角为
-2x+4在点(1,3)处的切线的倾斜角为
A.30° B.45° C.60° D.12°
(5)在△ABC中,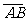 =c,
=c,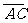 =b.若点D满足
=b.若点D满足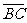 =2
=2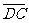 ,则
,则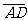 =
=
A.
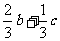 B.
B. 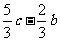 C.
C. 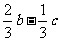 D.
D. 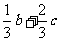
(6)y=(sinx-cosx)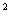 -1是
-1是
A.最小正周期为2π的偶像函数 B.最小正周期为2π的奇函数
C.最小正周期为π的偶函数 D.最小正周期为π的奇函数
(7)已知等比数列{a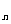 }满足a
}满足a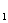 +a
+a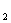 =3,a
=3,a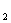 + a
+ a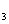 =6,则a
=6,则a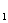 =
=
A.64 B.81 C.128 D.243
(8)若函数y=f(x)的图像与函数y=1n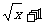 的图像关于直线y=x对称,则f(x)=
的图像关于直线y=x对称,则f(x)=
A.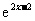 B.
B.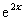 C.
C.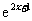 D.
D.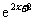
(9)为得到函数y=cos(x+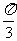 )的图像,只需将函数y=sinx的图像
)的图像,只需将函数y=sinx的图像
A.向左平移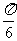 个长度单位 B.向右平移
个长度单位 B.向右平移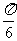 个长度单位
个长度单位
C.向左平移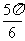 个长度单位 D.向右平移
个长度单位 D.向右平移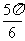 个长度单位
个长度单位
(10)若直线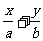 =1与圆
=1与圆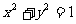 有公共点,则
有公共点,则
A.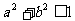 B.
B.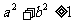 C.
C.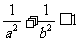 D.
D.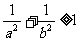
(11)已知三棱柱ABC-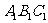 的侧棱与底面边长都相等,
的侧棱与底面边长都相等,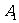 在底面ABC内的射影为△ABC的中心,则A
在底面ABC内的射影为△ABC的中心,则A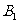 与底面ABC所成角的正弦值等于
与底面ABC所成角的正弦值等于
A.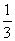 B.
B.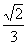 C.
C.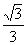 D.
D.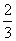
(12)将1,2,3填入3×3的方格中,要求每行、每列都没有重复数字,下面是一种填法,则不同的填写方法共有
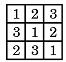
A.6种 B.12种 C.24种 D.48种
第Ⅱ卷
2.第Ⅱ卷共7页,请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,在试题卷上作答无效。
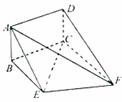
(18)(本题14分)如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF, BCF=
BCF= CEF=
CEF=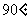 ,AD=
,AD=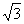 ,EF=2。
,EF=2。
(Ⅰ)求证:AE//平面DCF;
(Ⅱ)当AB的长为何值时,二面角A-EF-C的大小为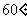 ?
?
(19)(本题14分)一个袋中有若干个大小相同的黑球、白球和红球。已知从袋中任意摸出1个球,得到黑球的概率是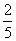 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是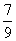 。
。
(Ⅰ)若袋中共有10个球,
(i)求白球的个数;
(ii)从袋中任意摸出3个球,记得到白球的个数为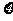 ,求随机变量
,求随机变量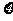 的数学期望
的数学期望 。
。
(Ⅱ)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于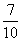 。并指出袋中哪种颜色的球个数最少。
。并指出袋中哪种颜色的球个数最少。
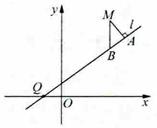
(20)(本题15分)已知曲线C是到点P(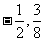 )和到直线
)和到直线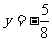 距离相等的点的轨迹。
距离相等的点的轨迹。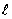 是过点Q(-1,0)的直线,M是C上(不在
是过点Q(-1,0)的直线,M是C上(不在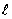 上)的动点;A、B在
上)的动点;A、B在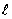 上,
上,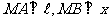 轴(如图)。
轴(如图)。
(Ⅰ)求曲线C的方程;
(Ⅱ)求出直线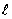 的方程,使得
的方程,使得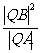 为常数。
为常数。
(21)(本题15分)已知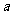 是实数,函数
是实数,函数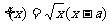 。
。
(Ⅰ)求函数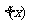 的单调区间;
的单调区间;
(Ⅱ)设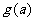 为
为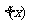 在区间
在区间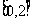 上的最小值。
上的最小值。
(i)写出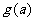 的表达式;
的表达式;
(ii)求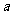 的取值范围,使得
的取值范围,使得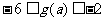 。
。
(22)(本题14分)已知数列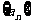 ,
,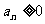 ,
,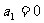 ,
,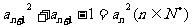 .记
.记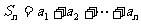 .
.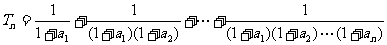 .
.
求证:当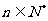 时,
时,
(Ⅰ)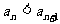 ;
;
(Ⅱ)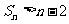 ;
;
(Ⅲ)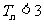 。
。
(11)已知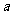 >0,若平面内三点A(1,-
>0,若平面内三点A(1,-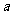 ),B(2,
),B(2,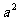 ),C(3,
),C(3,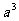 )共线,则
)共线,则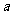 =
。
=
。
(12)已知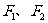 为椭圆
为椭圆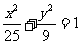 的两个焦点,过
的两个焦点,过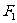 的直线交椭圆于A、B两点
的直线交椭圆于A、B两点
若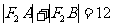 ,则
,则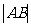 =
。
=
。
(13)在△ABC中,角A、B、C所对的边分别为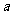 、b、c ,若
、b、c ,若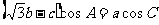 ,则
,则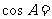 。
。
(14)如图,已知球O点面上四点A、B、C、D,DA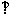 平面ABC,AB
平面ABC,AB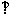 BC,DA=AB=BC=
BC,DA=AB=BC=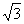 ,则球O点体积等于 。
,则球O点体积等于 。
(15)已知t为常数,函数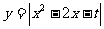 在区间[0,3]上的最大值为2,则t= 。
在区间[0,3]上的最大值为2,则t= 。
(16)用1,2,3,4,5,6组成六位数(没有重复数字),要求任何相邻两个数字的奇偶性不同,且1和2相邻,这样的六位数的个数是 (用数字作答)。
(17)若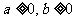 ,且当
,且当 时,恒有
时,恒有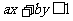 ,则以
,则以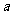 ,b为坐标点P(
,b为坐标点P(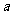 ,b)所形成的平面区域的面积等于 。
,b)所形成的平面区域的面积等于 。
(1)已知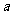 是实数,
是实数,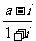 是纯虚数,则
是纯虚数,则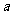 =
=
(A)1
(B)-1 (C)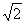 (D)-
(D)-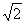
(2)已知U=R,A=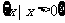 ,B=
,B=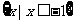 ,则(A
,则(A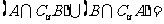
(A)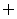 (B)
(B)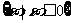
(C)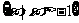 (D)
(D)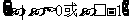
(3)已知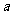 ,b都是实数,那么“
,b都是实数,那么“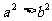 ”是“
”是“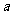 >b”的
>b”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(4)在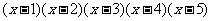 的展开式中,含
的展开式中,含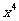 的项的系数是
的项的系数是
(A)-15 (B)85 (C)-120 (D)274
(5)在同一平面直角坐标系中,函数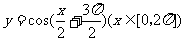 的图象和直线
的图象和直线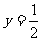 的交点个数是
的交点个数是
(A)0 (B)1 (C)2 (D)4
(6)已知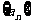 是等比数列,
是等比数列,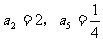 ,则
,则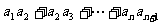 =
=
(A)16(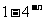 )
(B)16(
)
(B)16(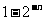 )
)
(C)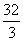 (
(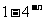 )
(D)
)
(D)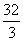 (
(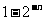 )
)
(7)若双曲线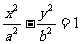 的两个焦点到一条准线的距离之比为3:2,则双曲线的离心率是
的两个焦点到一条准线的距离之比为3:2,则双曲线的离心率是
(A)3 (B)5
(C)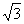 (D)
(D)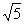
(8)若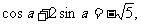 则
则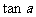 =
=
(A)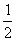 (B)2
(C)
(B)2
(C)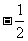 (D)
(D)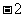
(9)已知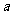 ,b是平面内两个互相垂直的单位向量,若向量
,b是平面内两个互相垂直的单位向量,若向量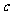 满足
满足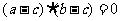 ,则
,则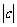 的最大值是
的最大值是
(A)1 (B)2
(C)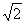 (D)
(D)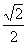
(10)如图,AB是平面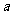 的斜线段,A为斜足,若点P在平面
的斜线段,A为斜足,若点P在平面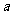 内运动,使得△ABP的面积为定值,则动点P的轨迹是
内运动,使得△ABP的面积为定值,则动点P的轨迹是
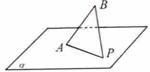
(A)圆 (B)椭圆
(C)一条直线 (D)两条平行直线
第Ⅱ卷(共100分)
20.若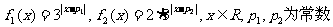
且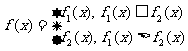
(1)求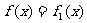 对所有实数
对所有实数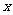 成立的充要条件(用
成立的充要条件(用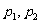 表示)
表示)
(2)设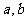 为两实数,
为两实数,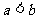 且
且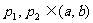 若
若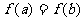
求证: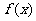 在区间
在区间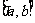 上的单调增区间的长度和为
上的单调增区间的长度和为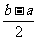 (闭区间
(闭区间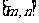 的长度定义为
的长度定义为 )
)
19.(1)设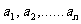 是各项均不为零的等差数列(
是各项均不为零的等差数列( ),且公差
),且公差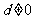 ,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列:
,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列:
①当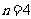 时求
时求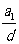 的数值②求
的数值②求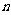 的所有可能值;
的所有可能值;
(2)求证:对于一个给定的正整数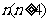 ,存在一个各项及公差都不为零的等差数列
,存在一个各项及公差都不为零的等差数列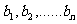 ,其中任意三项(按原来顺序)都不能组成等比数列。
,其中任意三项(按原来顺序)都不能组成等比数列。
18.设平面直角坐标系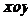 中,设二次函数
中,设二次函数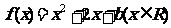 的图像与两坐标轴有三个交点,经过这三个交点的圆记为
的图像与两坐标轴有三个交点,经过这三个交点的圆记为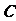 。求:
。求:
(1)求实数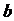 的取值范围
的取值范围
(2)求圆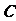 的方程
的方程
(3)问圆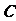 是否经过某定点(其坐标与
是否经过某定点(其坐标与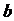 无关)?请证明你的结论。
无关)?请证明你的结论。
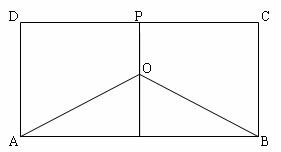
17.某地有三家工厂,分别位于矩形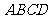 的顶点
的顶点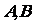 及
及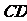 的中点
的中点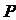 处,已知
处,已知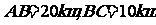 ,为了处理三家工厂的污水,现要在矩形
,为了处理三家工厂的污水,现要在矩形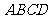 的区域上(含边界),且
的区域上(含边界),且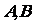 与等距离的一点
与等距离的一点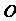 处建造一个污水处理厂,并铺设排污管道
处建造一个污水处理厂,并铺设排污管道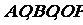 ,设排污管道的总长为
,设排污管道的总长为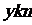
(1)按下列要求写出函数关系式:
①设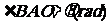 ,将
,将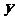 表示成
表示成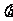 的函数关系式
的函数关系式
②设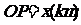 ,将
,将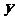 表示成
表示成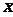 的函数关系式
的函数关系式
(2)请你选用(1)中的一个函数关系式,确定污水处理厂的位置,使三条排污管道总长度最短。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com