
21.(本小题满分12分)
设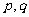 为实数,
为实数,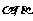 是方程
是方程 的两个实根,数列
的两个实根,数列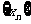 满足
满足 ,
,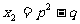 ,
,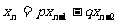

(1)证明: ,
,
(2)求数列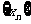 的通项公式;
的通项公式;
(3)若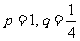 ,求
,求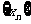 的前
的前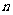 项和
项和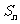 .
.
20.(本小题满分14分)
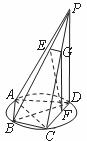
如图所示,四棱锥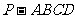 的底面
的底面 是半径为
是半径为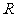 的圆的内接四边形,其中
的圆的内接四边形,其中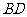 是圆的直径,
是圆的直径,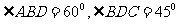 ,
,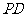 垂直底面
垂直底面 ,
,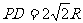 ,
,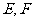 分别是
分别是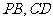 上的点,且
上的点,且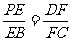 ,过点
,过点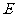 作
作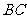 的平行线交
的平行线交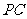 于
于 .
.
(1)求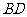 与平面
与平面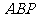 所成角
所成角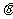 的正弦值;
的正弦值;
(2)证明: 是直角三角形;
是直角三角形;
(3)当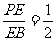 时,求
时,求 的面积.
的面积.
19.(本小题满分14分)
设 ,函数
,函数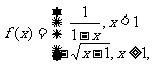
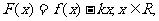 试讨论函数
试讨论函数 的单调性.
的单调性.
18.(本小题满分14分)
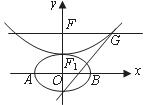
设 ,椭圆方程为
,椭圆方程为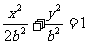 ,抛物线方程为
,抛物线方程为 .如图所示,过点
.如图所示,过点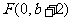 作
作 轴的平行线,与抛物线在第一象限的交点为
轴的平行线,与抛物线在第一象限的交点为 ,已知抛物线在点
,已知抛物线在点 的切线经过椭圆的右焦点
的切线经过椭圆的右焦点 .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设 分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点P,使得
分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点P,使得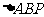 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
17.(本小题满分13分)
随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元.设1件产品的利润(单位:万元)为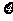 .
.
(1)求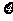 的分布列;
的分布列;
(2)求1件产品的平均利润(即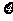 的数学期望);
的数学期望);
(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
16.(本小题满分13分)
已知函数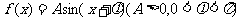 ,
,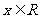 的最大值是1,其图像经过点
的最大值是1,其图像经过点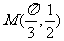 .
.
(1)求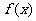 的解析式;
的解析式;
(2)已知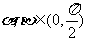 ,且
,且 ,求
,求 的值.
的值.
15.(几何证明选讲选做题)已知PA是圆O的切线,切点为A,PA=2.AC是圆O的直径,PC与圆O交于点B,PB=1,则圆O的半径R= .
14.(不等式选讲选做题)已知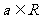 ,若关于
,若关于 的方程
的方程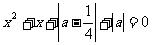 有实根,则
有实根,则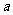 的取值范围是
.
的取值范围是
.
13.(坐标系与参数方程选做题)已知曲线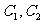 的极坐标方程分别为
的极坐标方程分别为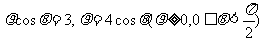 ,则曲线
,则曲线 与
与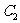 交点的极坐标为
.
交点的极坐标为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com