
6.古代“五行”学说认为:“物质分金、木、水、火、土五种属性,金克木、木克土,土克水,水克火,火克金”,从五种不同属性的物质中随机抽取两种,则抽取的两种物质不相克的概率 A.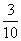 B.
B.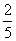 C.
C.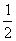 D.
D.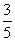
5.已知复数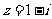 ,则
,则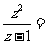
A. B.
B.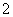 C.
C.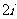 D.
D.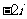
4.下列四个图各反映了两个变量的某种关系,其中可以看作具有较强线性相关关系的是

A.①③ B.①④ C.②③ D.①②④
3.已知函数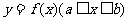 ,则集合
,则集合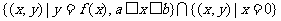 中含有元素的个数为
中含有元素的个数为
A. B.
B.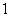 或
或 C.
C.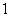 D.
D.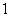 或
或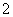
2.根据下边的结构图,总经理的直接下属是
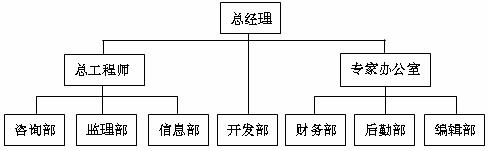
A.总工程师和专家办公室 B.开发部
C.总工程师、专家办公室和开发部 D.总工程师、专家办公室和所有七个部
1.定义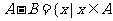 且
且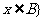 ,若
,若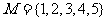 ,
,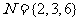 ,则
,则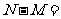
A.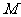 B.
B.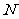 C.
C.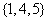 D.
D.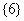
22.(本题满分14分)
设函数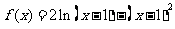 .
.
(Ⅰ)求函数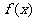 的单调递增区间;
的单调递增区间;
(Ⅱ)若关于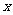 的方程
的方程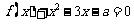 在区间
在区间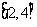 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数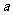 的取值范围.
的取值范围.
21.(本题满分12分)
某工厂在试验阶段大量生产一种零件.这种零件有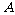 、
、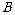 两项技术指标需要检测,设各项技术指标达标与否互不影响.若
两项技术指标需要检测,设各项技术指标达标与否互不影响.若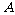 项技术指标达标的概率为
项技术指标达标的概率为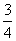 ,有且仅有一项技术指标达标的概率为
,有且仅有一项技术指标达标的概率为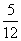 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品.
(Ⅰ)求一个零件经过检测为合格品的概率;
(Ⅱ)任意依次抽出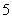 个零件进行检测,求其中至多
个零件进行检测,求其中至多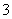 个零件是合格品的概率;
个零件是合格品的概率;
(Ⅲ)任意依次抽取该种零件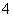 个,设
个,设 表示其中合格品的个数,求
表示其中合格品的个数,求 与
与 .
.
20.(本题满分12分)
已知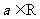 ,函数
,函数 .
.
(Ⅰ)如果函数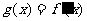 是偶函数,求
是偶函数,求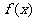 的极大值和极小值;
的极大值和极小值;
(Ⅱ)如果函数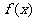 是
是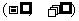 上的单调函数,求
上的单调函数,求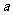 的取值范围.
的取值范围.
19.(本题满分12分)
已知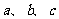 是互不相等的非零实数.用反证法证明三个方程
是互不相等的非零实数.用反证法证明三个方程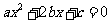 ,
, ,
,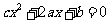 至少有一个方程有两个相异实根.
至少有一个方程有两个相异实根.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com