
24.(本小题满分10分)选修4-5:不等式选讲
设函数 .
.
(I)作出函数 的图象;
的图象;
(II)若不等式 的解集为
的解集为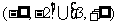 ,求
,求 值.
值.
23.(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: (
(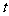 是参数).
是参数).
(I)将曲线C的极坐标方程和直线 参数方程转化为普通方程;
参数方程转化为普通方程;
(II)若直线l与曲线C相交于A、B两点,且 ,试求实数
,试求实数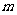 值.
值.
22.(本小题满分10分)选修4-1:几何证明选讲
|
(I)求证: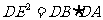 ;
;
(II)若⊙O的半径为 ,OB=
,OB= OE,求EF的长.
OE,求EF的长.

21.(本小题满分12分)
如图,已知曲线 从C上的点
从C上的点 作x轴的垂线,交
作x轴的垂线,交 轴的垂线,交C于点
轴的垂线,交C于点 设
设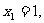
 ,
, .
.
(I)求Q1、Q2的坐标;
(II)求数列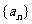 的通项公式;
的通项公式;
(III)记数列 的前n项和为
的前n项和为

请考生在第22,23,24三题中任选一题做答,如果多做,则按所做的第一题计分.
20.(本小题满分12分)
已知
(I)若a=3,求 的单调区间和极值;
的单调区间和极值;
(II)已知 是
是 的两个不同的极值点,且
的两个不同的极值点,且 ,若
,若
 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
19.(本小题满分12分)
从“神七”飞船带回的某种植物种子由于在太空中被辐射,我们把它们称作“太空种子”。这种“太空种子”成功发芽的概率为 ,发生基因突变的概率为
,发生基因突变的概率为 ,种子发芽与发生基因突变是两个相互独立事件.科学家在实验室对太空种子进行培育,从中选出优良品种。
,种子发芽与发生基因突变是两个相互独立事件.科学家在实验室对太空种子进行培育,从中选出优良品种。
(I)这种太空种子中的某一粒种子既发芽又发生基因突变的概率是多少?
(II)四粒这种太空种子中既发芽又发生基因突变的种子数为随机变量 ,求
,求 的概率分布列和数学期望
的概率分布列和数学期望 。
。
18.(本小题满分12分)
长方体ABCD-A1B1C1D1的侧棱AA1的长是a,底面ABCD的边长AB=2a,BC=a,E为C1D1的中点.
(I)求证:DE⊥平面BCE;
(II)求二面角E-BD-C的正切值.

17.(本小题满分12分)
已知 、
、 、
、 为锐角
为锐角 的三个内角,向量
的三个内角,向量
 ,
, 且
且 .
.
(Ⅰ)求 的大小;
的大小;
(Ⅱ)求 取最大值时,∠B的大小.
取最大值时,∠B的大小.
16.双曲线
 的离心率是2,则
的离心率是2,则 的最小值是 .
的最小值是 .
15.设点P是曲线 上的任意一点,曲线在P点处切线的倾斜角为α,则角α的取值范围是
.
上的任意一点,曲线在P点处切线的倾斜角为α,则角α的取值范围是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com