
5.已知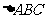 ,
, 为平面内一点,且设
为平面内一点,且设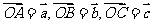 ,则满足条件
,则满足条件
 时,
时, 是
是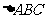 的 ( )
的 ( )
A.内心 B.外心 C.垂心 D.重心
4.设向量 与
与 的夹角为
的夹角为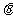 ,
,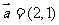 ,
,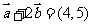 ,则
,则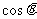 等于 ( )
等于 ( )
A.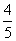 B.
B.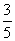 C.
C.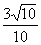 D.
D.
3.已知角 的终边上一点的坐标为
的终边上一点的坐标为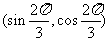 ,则角
,则角 的最小正值为 ( )
的最小正值为 ( )
A.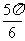 B.
B.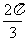 C.
C.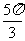 D.
D.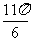
2.下列几何体各自的三视图中,有且仅有两个视图相同的是 ( )

A.①② B.①③ C.①④ D.②④
1.若集合 ,
,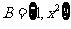 ,
,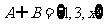 ,则满足条件的实数
,则满足条件的实数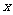 的个数为( )
的个数为( )
A.1个 B.2个 C.3个 D.4个
21.(本小题满分12分)
已知数列{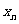 }满足:
}满足: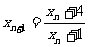 ,
,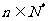 ,
, 。
。
(1)是否存在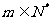 ,使
,使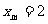 ,并说明理由;
,并说明理由;
(2)试比较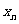 与2的大小关系;
与2的大小关系;
(3)设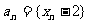 ,
, 为数列{
为数列{ }前
}前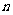 项和,求证:当
项和,求证:当 时,
时, 。
。
20.(本小题满分12分)
已知曲线C上任意一点M到点F(0,1)的距离比它到直线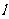 :
: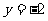 的距离小1。
的距离小1。
(1)求曲线C的方程;
(2)若过点P(2,2)的直线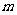 与曲线C交于A、B两点,设
与曲线C交于A、B两点,设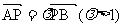 ,且△AOB的面积为
,且△AOB的面积为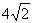 (O为坐标原点),求实数
(O为坐标原点),求实数 的值。
的值。
19.(本小题满分12分)
已知函数 ,
, 。
。
(1)求函数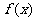 的单调区间;
的单调区间;
(2)如果关于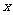 的方程
的方程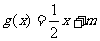 有实数根,求实数
有实数根,求实数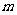 的取值范围。
的取值范围。
18.(本小题满分13分)
如下图,直四棱柱ABCD-A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC∩BD=O,A1C1∩B1D1=O1,E是O1A的中点。
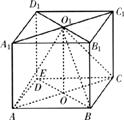
(1)求证:平面O1AC⊥平面O1BD;
(2)求二面角O1-BC-D的大小;
(3)求点E到平面O1BC的距离。
17.(本小题满分13分)
一种电脑屏幕保护画面,只有符号“○”和“×”随机地反复出现,每秒钟变化一次,每次变化只出现“○”和“×”之一,其中出现“○”的概率为 ,出现“×”的概率为
,出现“×”的概率为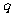 。若第
。若第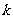 次出现“○”,则记
次出现“○”,则记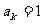 ;出现“×”,则记
;出现“×”,则记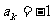 ,令
,令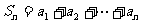 。
。
(1)当 时,记
时,记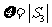 ,求
,求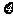 的分布列及数学期望;
的分布列及数学期望;
(2)当 时,求
时,求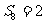 且
且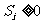 (
(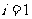 ,2,3,4)的概率。
,2,3,4)的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com