
21.(本小题满分12分)
数列{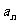 }的各项均为正数,
}的各项均为正数, 为其前
为其前 项和,对于任意
项和,对于任意 ,总有
,总有 。
。
(1)求数列{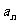 }的通项公式;
}的通项公式;
(2)设正数数列{ }满足
}满足 ,(
,( ),求数列{
),求数列{ }中的最大项;
}中的最大项;
(3)求证: 。
。
20.(本小题满分12分)
在平面直角坐标系中,O为坐标原点,设直线 经过点P(3,
经过点P(3, ),且与
),且与 轴交于点F(2,0)。
轴交于点F(2,0)。
(1)求直线 的方程;
的方程;
(2)如果一个椭圆经过点P,且点F为它的一个焦点,求椭圆的标准方程;
(3)若在(1)、(2)情形下,设直线 与椭圆的另一个交点为Q,且
与椭圆的另一个交点为Q,且 ,当
,当 最小时,求
最小时,求 对应的值。
对应的值。
19.(本小题满分12分)
已知定义在R上的函数 ,其中
,其中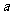 为常数。
为常数。
(1)若 是函数
是函数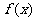 的一个极值点,求
的一个极值点,求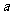 的值;
的值;
(2)若函数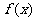 在区间(-1,0)上是增函数,求
在区间(-1,0)上是增函数,求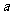 的取值范围;
的取值范围;
(3)若函数 ,在
,在 处取得最大值,求正数
处取得最大值,求正数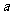 的取
的取
值范围。
18.(本小题满分13分)
已知等腰梯形PDCB中(如下图1),PB= ,DC=1,PD=BC=
,DC=1,PD=BC= ,A为PB边上一点,且PA=1,将APAD沿AD折起,使面PAD⊥面ABCD(如下图2)。
,A为PB边上一点,且PA=1,将APAD沿AD折起,使面PAD⊥面ABCD(如下图2)。


(1)证明:面PAD⊥面PCD;
(2)求二面角D-PC-B的大小。
17.(本小题满分13分)
某足球俱乐部2009年2月份安排4次体能测试,规定:按顺序测试,一旦测试合格就不必参加以后的测试,否则继续参加后面的测试。若运动员小李4次测试每次合格的概率组成一个公差为 的等差数列,他第一次测试合格的概率不超过
的等差数列,他第一次测试合格的概率不超过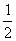 ,且他直到第二次测试才合格的概率为
,且他直到第二次测试才合格的概率为 。
。
(1)求小李第一次参加测试就合格的概率 ;
;
(2)求小李2月份参加测试的次数 的分布列和数学期望。
的分布列和数学期望。
16.(本小题满分13分)
在△ABC中,已知角A、B、C所对的三条边分别是 ,且
,且 。
。
(1)求证: ;
;
(2)求函数 的值域。
的值域。
15.从数字1,2,3…10中按由小到大的顺序取出 且
且 ,
, ,则不同的取法有__________种。
,则不同的取法有__________种。
14. 是偶函数,
是偶函数, 是奇函数,那么
是奇函数,那么 的值是__________。
的值是__________。
13.已知球O的表面积为 ,A、B、C三点都在球面上,且任意两点间的球面距离为
,A、B、C三点都在球面上,且任意两点间的球面距离为 ,则OA与平面ABC所成角的正切值是__________。
,则OA与平面ABC所成角的正切值是__________。
12.某集团生产了一·种新型电子元件,现从中随机抽取200个进行寿命试验,得到频率分布直方图如下图所示,估计寿命在100-400小时的概率__________。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com