
5、已知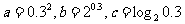 ,则a,b,c的大小关系是 ( )
,则a,b,c的大小关系是 ( )
A 、a>b>c B 、b>a>c C 、b>c>a D、 c>b>a
4、函数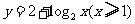 的值域为
( )
的值域为
( )
A、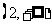 B、
B、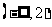 C、
C、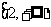 D、
D、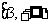
3、函数f(x)=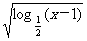 的定义域是
( )
的定义域是
( )
A、(1,+∞) B、(2,+∞) C、(-∞,2) D、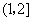
2、在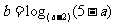 中,实数
中,实数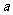 的取值范围是
( )
的取值范围是
( )
A、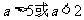 B、
B、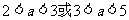 C、
C、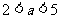 D、
D、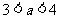
1、有以下四个结论 1 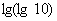 =0 2
=0 2 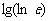 =0 3若10=
=0 3若10=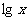 ,则x=10 4 若e=
,则x=10 4 若e=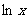 ,则x=e2, 其中正确的是 ( )
,则x=e2, 其中正确的是 ( )
A.13 B.24 C.12 D. 34
(二)课堂练习
(一) .回顾与总结
1、完成下表(指、对数函数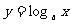
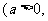 且
且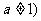 的图象和性质)
的图象和性质)
|
|
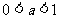 |
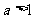 |
|
|
图 象 |
|
|
|
|
定义域 |
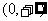 |
||
|
值域 |
R |
||
|
性 质 |
(1)过定点(0,1),即x=1时,y=0
|
2.已知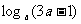 恒为正数,求
恒为正数,求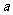 的取值范围.
的取值范围.
解:(略)
[总结点评]:(由学生独立思考,师生共同归纳概括).
3.求函数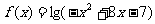 的定义域及值域.
的定义域及值域.
解:(略)
注意:函数值域的求法.
4.(1)函数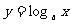 在[2,4]上的最大值比最小值大1,求
在[2,4]上的最大值比最小值大1,求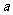 的值;
的值;
(2)求函数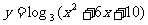 的最小值.
的最小值.
解:(略)
注意:利用函数单调性求函数最值的方法,复合函数最值的求法.
5.(2003年上海高考题)已知函数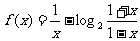 ,求函数
,求函数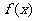 的定义域,并讨论它的奇偶性和单调性.
的定义域,并讨论它的奇偶性和单调性.
解:(略)
注意:判断函数奇偶性和单调性的方法,规范判断函数奇偶性和单调性的步骤.
6.求函数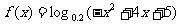 的单调区间.
的单调区间.
解:(略)
注意:复合函数单调性的求法及规律:“同增异减”.
练习:求函数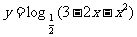 的单调区间.
的单调区间.
重点:对数函数的图象和性质.
难点:对对数函数的性质的综合运用.
(1)进一步理解对数函数的图象和性质;
(2)熟练应用对数函数的图象和性质,解决一些综合问题;
(3)通过例题和练习的讲解与演练,培养学生分析问题和解决问题的能力。
11、求下列函数的定义域
(1)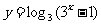 (2)
(2)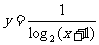
(3)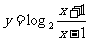
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com