
1、理解集合之间包含与相等的含义,能识别给定集合的子集,培养学生分析、比较、归纳的逻辑思维能力.
(四).作业:P59 习题2.1 A组第5题
(三).归纳小结
1、理解指数函数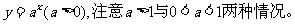
2、解题利用指数函数的图象,可有利于清晰地分析题目,培养数型结合与分类讨论的数学思想 .
(二).讲授新课
1、指数函数的定义:
一般地,函数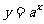 (
(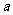 >0且
>0且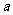 ≠1)叫做指数函数,其中
≠1)叫做指数函数,其中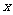 是自变量,函数的定义域为R.
是自变量,函数的定义域为R.
2、指数函数定义中为什么规定底数a满足条件a>0且a≠1?
①
②若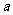 <0,如
<0,如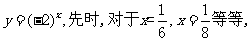 在实数范围内的函数值不存在.
在实数范围内的函数值不存在.
③若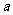 =1,
=1, 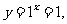 是一个常量,没有研究的意义,只有满足
是一个常量,没有研究的意义,只有满足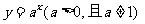 的形式才能称为指数函数,
的形式才能称为指数函数,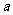 为常数,像
为常数,像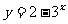 ,
,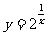 ,
,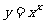 ,
,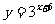 ,
,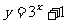 等等,不符合
等等,不符合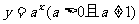 的形式,所以不是指数函数.
的形式,所以不是指数函数.
3、我们在学习函数的单调性的时候,主要是根据函数的图象,即用数形结合的方法来研究.
完成以下表格,并且画出函数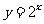 和
和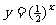 的图象
的图象
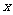 |
-2.00 |
-1.50 |
-1.00 |
-0.50 |
0 |
0.50 |
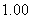 |
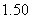 |
2.00 |
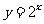 |
|
0.35 |
|
0.71 |
|
1.41 |
|
2.83 |
|
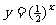 |
|
2.83 |
|
1.41 |
|
0.71 |
|
0.35 |
|










|
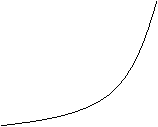
4、问题1:从图上看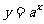 (
(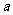 >1)与
>1)与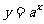 (0<
(0<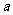 <1)两函数图象的特征.
<1)两函数图象的特征. 
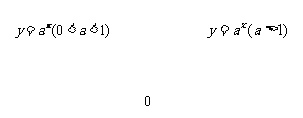 问题2:根据函数的图象研究函数的定义域、值域、特殊点、单调性、最大(小)值、奇偶性.
问题2:根据函数的图象研究函数的定义域、值域、特殊点、单调性、最大(小)值、奇偶性.
|
图象特征 |
函数性质 |
||
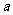 >1 >1 |
0<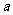 <1 <1 |
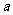 >1 >1 |
0<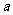 <1 <1 |
向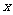 轴正负方向无限延伸 轴正负方向无限延伸 |
函数的定义域为R |
||
图象关于原点和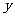 轴不对称 轴不对称 |
非奇非偶函数 |
||
函数图象都在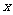 轴上方 轴上方 |
函数的值域为R+ |
||
|
函数图象都过定点(0,1) |
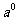 =1 =1 |
||
|
自左向右, 图象逐渐上升 |
自左向右, 图象逐渐下降 |
增函数 |
减函数 |
|
在第一象限内的图 象纵坐标都大于1 |
在第一象限内的图 象纵坐标都小于1 |
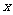 >0, >0,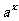 >1 >1 |
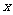 >0, >0,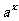 <1 <1 |
|
在第二象限内的图 象纵坐标都小于1 |
在第二象限内的图 象纵坐标都大于1 |
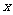 <0, <0,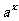 <1 <1 |
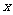 <0, <0,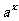 >1 >1 |
例题:
例1:求下列函数的定义域:(1)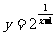 (2)
(2)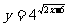
分析:类为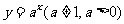 的定义域是R,所以,要使(1),(2)题的定义域,保要使其指数部分有意义就可以.
的定义域是R,所以,要使(1),(2)题的定义域,保要使其指数部分有意义就可以.
课堂练习:P58 练习:第2题
例2:(P56
例6)已知指数函数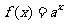 (
(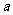 >0且
>0且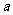 ≠1)的图象过点(3,π),求
≠1)的图象过点(3,π),求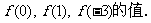
分析:要求 再把0,1,3分别代入
再把0,1,3分别代入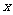 ,即可求得
,即可求得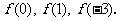
提问:要求出指数函数,需要几个条件?
例3:某种细胞分裂时,由1个分裂成2个,2个分裂成4个……依此类推,写出1个这样的细胞分裂x次后,得到的细胞个数y与x得函数解析式。
课堂练习:P59 习题2.1 A组第6题
补充练习:1、函数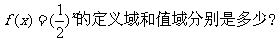
2、当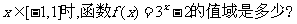
解(1)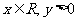 (2)(-
(2)(-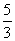 ,1)
,1)
(一). 情境设置
①在本章的开头,问题(1)中时间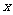 与GDP值中的
与GDP值中的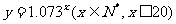 与问题(2)
与问题(2) ,请问这两个函数有什么共同特征.
,请问这两个函数有什么共同特征.
②这两个函数有什么共同特征
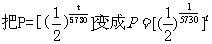 ,从而得出这两个关系式中的底数是一个正数,自变量为指数,即都可以用
,从而得出这两个关系式中的底数是一个正数,自变量为指数,即都可以用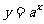 (
(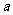 >0且
>0且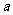 ≠1来表示).
≠1来表示).
重点:指数函数的概念和性质及其应用。
难点:指数函数性质的归纳,概括及其应用。
(1)通过实际问题了解指数函数的实际背景;
(2)理解指数函数的概念和意义,根据图象理解和掌握指数函数的性质.
(3)体会具体到一般数学讨论方式及数形结合的思想;
2、当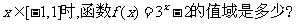
作业:P59 习题2.1 A组第5题
4、问题1: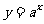 (
(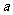 >1)与
>1)与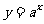 (0<
(0<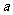 <1)两函数图象的特征.
<1)两函数图象的特征.
问题2:根据函数的图象研究函数的定义域、值域、特殊点、单调性、最大(小)值、奇偶性.
 图象特征 图象特征 |
函数性质 |
||
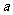 >1 >1 |
0<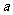 <1 <1 |
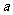 >1 >1 |
0<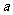 <1 <1 |
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
例题:例1:求下列函数的定义域:(1)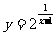 (2)
(2)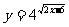
课堂练习:P58 练习:第2题
例2:已知指数函数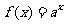 (
(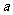 >0且
>0且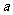 ≠1)的图象过点(3,π),求
≠1)的图象过点(3,π),求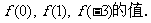
例3:某种细胞分裂时,由1个分裂成2个,2个分裂成4个……依此类推,写出1个这样的细胞分裂x次后,得到的细胞个数y与x得函数解析式。
课堂练习:P59 习题2.1 A组第6题
补充练习:1、函数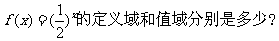
3、完成以下表格,并且画出函数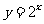 和
和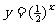 的图象
的图象
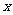 |
-2.00 |
-1.50 |
-1.00 |
-0.50 |
0 |
0.50 |
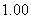 |
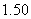 |
2.00 |
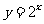 |
|
0.35 |
|
0.71 |
|
1.41 |
|
2.83 |
|
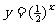 |
|
2.83 |
|
1.41 |
|
0.71 |
|
0.35 |
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com