
2、指数函数定义中为什么规定底数a满足条件a>0且a≠1
1、 指数函数的定义是什么
6、已知函数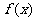 ,
,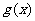 同时满足:
同时满足: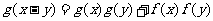 ;
;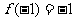 ,
,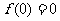 ,
,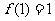 ,求
,求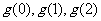 的值.
的值.
5、动点P从边长为1的正方形ABCD的顶点出发顺次经过B、C、D再回到A;设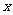 表示P点的行程,
表示P点的行程,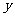 表示PA的长,求
表示PA的长,求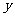 关于
关于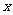 的函数解析式.
的函数解析式.
4、设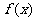 是抛物线,并且当点
是抛物线,并且当点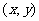 在抛物线图象上时,点
在抛物线图象上时,点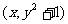 在函数
在函数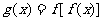 的图象上,求
的图象上,求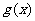 的解析式.
的解析式.
3、已知函数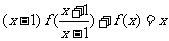 ,其中
,其中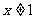 ,求函数解析式.
,求函数解析式.
2、在同一坐标系中绘制函数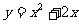 ,
,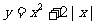 得图象.
得图象.
(1)函数的概念:设A、B是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数.记作: y=f(x),x∈A.其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合{f(x)| x∈A }叫做函数的值域.
(2)构成函数的三要素是什么?
定义域、对应关系和值域
(3)区间的概念
①区间的分类:开区间、闭区间、半开半闭区间;
②无穷区间;
③区间的数轴表示.
几类函数的定义域:
(1)如果f(x)是整式,那么函数的定义域是实数集R .
(2)如果f(x)是分式,那么函数的定义域是使分母不等于零的实数的集合 .
(3)如果f(x)是二次根式,那么函数的定义域是使根号内的式子大于或等于零的实数的集合.
(4)如果f(x)是由几个部分的数学式子构成的,那么函数定义域是使各部分式子都有意义的实数集合.(即求各集合的交集)
(5)满足实际问题有意义.
1、①求函数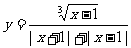 的定义域;
的定义域;
②求函数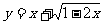 的值域。
的值域。
定义域值域的求法
学会用集合与对应的语言来刻画函数,理解函数符号y=f(x)的含义;了解函数构成的 三要素,了解映射的概念;体会函数是一种刻画变量之间关系的重要数学模型,体会对应关系在刻画函数概念中的作用;会求一些简单函数的定义域和值域,并熟练使用区间表示法 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com