
21.(本小题满分14分)给定实数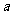 (
(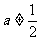 ),设函数
),设函数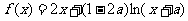 (
(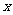 >
> ,
,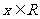 ),
),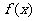 的导数
的导数 的图像为
的图像为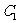 ,
,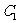 关于直线
关于直线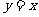 对称的图像记为
对称的图像记为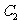 .
.
(Ⅰ)求函数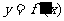 的单调区间;
的单调区间;
(Ⅱ)对于所有整数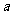 (
( ),
),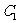 与
与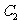 是否存在纵坐标和横坐标都是整数的公共点?若存在,请求出公共点的坐标;若不若存在,请说明理由.
是否存在纵坐标和横坐标都是整数的公共点?若存在,请求出公共点的坐标;若不若存在,请说明理由.
[答案及详细解析]
20.(本小题满分14分)已知数列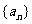 的前n项和
的前n项和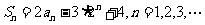 .
.
(Ⅰ)求数列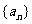 的通项公式;
的通项公式;
(Ⅱ)设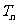 为数列
为数列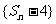 的前n项和,求
的前n项和,求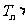
19.(本小题满分14分)在直角坐标平面内,定点 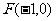 、
、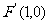 ,动点M,满足条件
,动点M,满足条件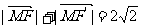 .
.
(Ⅰ)求动点M的轨迹C的方程;
(Ⅱ)过点F的直线交曲线C交于A,B两点,求以AB为直径的圆的方程,并判定这个圆与直线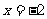 的位置关系.
的位置关系.
18.(本小题满分13分)如图,已知直四棱柱ABCD-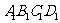 的底面是边长为2、
的底面是边长为2、
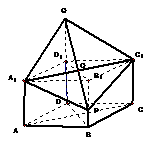
∠ADC=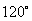 的菱形,
的菱形,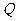 是侧棱
是侧棱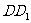 (
(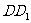 >
>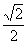 )延长线上的一点,过点
)延长线上的一点,过点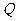 、
、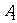 、
、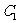 作菱形截面
作菱形截面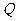
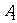
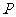
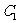 交侧棱
交侧棱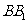 于点P.设截面
于点P.设截面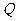
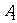
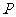
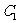 的面积为
的面积为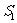 ,四面体
,四面体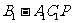 的三侧面
的三侧面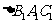 、
、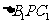 、
、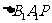 面积的和为
面积的和为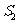 ,
,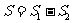 .
.
(Ⅰ)证明: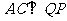 ;
;
(Ⅱ) 当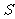 取得最小值时,求
取得最小值时,求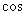 ∠
∠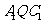 的值.
的值.
17.(本小题满分12分)班级联欢时,主持人拟出了如下一些节目:跳双人舞、独唱、朗诵等,指定3个男生和2个女生来参与,把5个人分别编号为1,2,3,4,5,其中1,2,3号是男生,4,5号是女生,将每个人的号分别写在5张相同的卡片上,并放入一个箱子中充分混合,每次从中随机地取出一张卡片,取出谁的编号谁就参与表演节目.
(I)为了选出2人来表演双人舞,连续抽取2张卡片,求取出的2人不全是男生的概率;
(Ⅱ)为了选出2人分别表演独唱和朗诵,抽取并观察第一张卡片后,又放回箱子中,
充分混合后再从中抽取第二张卡片,求:独唱和朗诵由同一个人表演的概率.
16.(本小题满分13分)如图所示,正在亚丁湾执行护航任务的某导弹护卫舰,突然收到一艘商船的求救信号,紧急前往相关海域.到达相关海域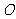 处后发现,在南偏西
处后发现,在南偏西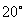 、5海里外的洋面M处有一条海盗船,它正以每小时20海里的速度向南偏东
、5海里外的洋面M处有一条海盗船,它正以每小时20海里的速度向南偏东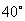 的方向逃窜.某导弹护卫舰当即施放载有突击队员的快艇进行拦截,快艇以每小时30海里的速度向南偏东
的方向逃窜.某导弹护卫舰当即施放载有突击队员的快艇进行拦截,快艇以每小时30海里的速度向南偏东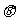 的方向全速追击.请问:快艇能否追上海盗船?如果能追上,请求出
的方向全速追击.请问:快艇能否追上海盗船?如果能追上,请求出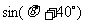 的值;如果未能追上,请说明理由.(假设海面上风平浪静、海盗船逃窜的航向不变、快艇运转正常无故障等)
的值;如果未能追上,请说明理由.(假设海面上风平浪静、海盗船逃窜的航向不变、快艇运转正常无故障等)

(二)选做题(14-15题,考生只能从中选做一题)
14. (坐标系与参数方程选做题)设曲线
(坐标系与参数方程选做题)设曲线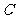 的参数方程为
的参数方程为 是参数,
是参数, ),若曲线C与直线
),若曲线C与直线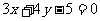 只有一个交点,则实数
只有一个交点,则实数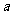 的值是____________.
的值是____________.
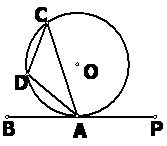
15.(几何证明选讲选做题)如右图,已知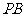 是⊙
是⊙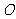 的
的
切线,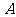 是切点,
是切点,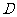 是弧
是弧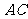 上一点,若
上一点,若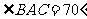 ,
,
则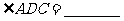 .
.
(一)必做题(11-13题)
11.函数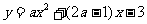 在区间[
在区间[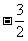 ,2]上的最大值是3,则实数
,2]上的最大值是3,则实数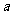 =____________.
=____________.
12.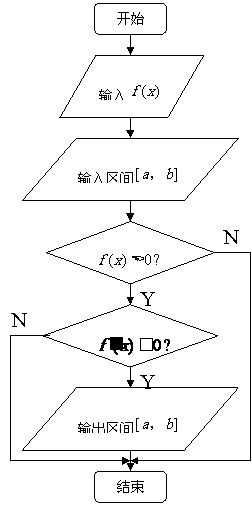 关于函数
关于函数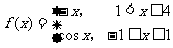 的流程图如右,现输入区间
的流程图如右,现输入区间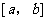 ,则输出的区间是____________.
,则输出的区间是____________.
13.设平面上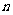 个圆周最多把平面分成
个圆周最多把平面分成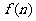 片(平面区域),则
片(平面区域),则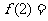 ____________,
____________,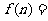 ____________.(
____________.(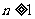 ,
,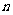 是自然数)
是自然数)
10.设正数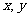 满足
满足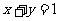 ,若不等式
,若不等式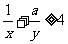 对任意的
对任意的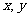 成立,则正实数
成立,则正实数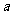 的取值范围是( )
的取值范围是( )
A .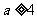 B.
B.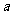 >1 C .
>1 C .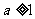 D.
D.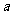 >4
>4
第Ⅱ卷(非选择题)
9.已知集合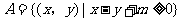 ,集合
,集合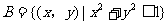 ,若
,若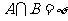 ,则实数
,则实数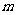 的取值范围是
的取值范围是
A.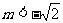 B.
B. C.
C.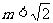 D.
D. 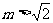
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com