
例3:设集合A={x|x2+4x=0,x∈R},B=
{x|x2+2(a+1)x+a2-1=0,x∈R},若B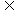 A,
A,
求实数a的取值范围.
分析:首先要弄清集合A中含有哪些元素,
在由B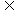 A,可知,集合B按元素的
A,可知,集合B按元素的
多少分类讨论即可.
[解]
A={x|x2+4x =0,x∈R}={0,-4}
∵
B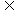 A
A
∴ B=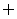 或{0},{-4},{0,-4}
或{0},{-4},{0,-4}
①当B=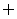 时,⊿=[2(a+1)]2-4•(a2-1)<0
时,⊿=[2(a+1)]2-4•(a2-1)<0
∴ a< -1
②当B={0}时,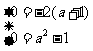
∴ a=-1
③当B={-4}时,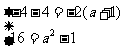
∴
a=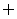
④当B={0,-4}时,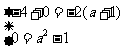
∴ a=1
∴ a的取值范围为:a<-1,或a=-1,或a=1.
点评:
B=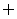 易被忽视,要提防这一点.
易被忽视,要提防这一点.
4.以下各组是什么关系,用适当的符号表来.
(1) 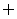 与{0}
(2) {-1,1}与{1,-1}
与{0}
(2) {-1,1}与{1,-1}
(3) {(a,b)} 与{(b,a)}
(4) 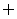 与{0,1,
与{0,1,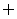 }
}
3.(1)已知{1,2 }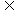 M
M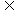 {1,2,3,4,
{1,2,3,4,
5},则这样的集合M有多少个?
(2)已知M={1,2,3,4,5,6, 7
,8,9},集合P满足:P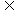 M,且
M,且
若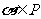 ,则10-
,则10-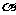 ∈P,则这样
∈P,则这样
的集合P有多少个?
2.指出下列各组中集合A与B之间的关系.
(1) A={-1,1},B=Z;
(2)A={1,3,5,15},B={x|x是15的正
约数};
 (3) A = N*,B=N
(3) A = N*,B=N
(4) A ={x|x=1+a2,a∈N*}
B={x|x=a2-4a+5,a∈N*}
例2:
以下各组是什么关系,用适当的符号表示出来.
(1)a与{a} 0 与 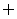
(2)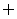 与{20,
与{20,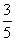 ,
,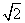 ,
,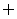 }
}
(3)S={-2,-1,1,2},A={-1,1},
B={-2,2};
(4)S=R,A={x|x≤0,x∈R},B={x|x>0 ,x∈R };
(5)S={x|x为地球人 },A={x|x 为中国人},B={x|x为外国人 }
[解]
点评:
① 判断两个集合的包含关系,主要是根据集合的子集,真子集的概念,看两个集合里的元素的关系,是包含,真包含,相等.
②元素与集合之间用_______________
集合与集合之间用_______________
追踪训练一
1.判断下列表示是否正确:
(1) a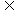 {a } (2) {a }∈{a,b }
{a } (2) {a }∈{a,b }
|
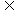 {b,a }
{b,a }
|

(5) 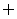 {-1,1}
{-1,1}
例1.
① 写出集合{a,b}的所有子集及其真子集;
② 写出集合{a,b,c}的所有子集及其真子集;
分析:按子集的元素的多少分别写出所有子集,这样才能达到不重复,无遗漏,
但应注意两个特殊的子集: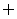 和本身.
和本身.
[解]
①集合{a,b}的所有子集为:
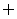 ,{a },{ b},{a,b};
,{a },{ b},{a,b};
②集合{a,b,c}的所有子集为:
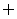 ,{a },{ b},{c},{a,b}
,{a },{ b},{c},{a,b}
{a,c},{b,c},{a,b,c}.
点评:写子集,真子集要按一定顺序来写.
①一个集合里有n个元素,那么它有2n个子集;
②一个集合里有n个元素,那么它有2n-1个真子集;
③一个集合里有n个元素,那么它有2n-2个非空真子集.
2.已知A={x|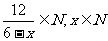 },试用列举法表示集合A.
},试用列举法表示集合A.
思维点拔:
例5. 已知集合B={x|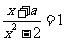 }有唯一元素,用列举法表示a的值构成的集合A.
}有唯一元素,用列举法表示a的值构成的集合A.
点拔:
本题集合B={x|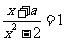 }有唯一元素,同学们习惯上将分式方程去分母,转化为一元二次方程的判别式为0,事实上当a=
}有唯一元素,同学们习惯上将分式方程去分母,转化为一元二次方程的判别式为0,事实上当a=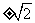 时,也能满足唯一元素,但方程已不是一元二次方程,而是一元一次方程,也有唯一解,所以本题要分三种情况讨论 .
时,也能满足唯一元素,但方程已不是一元二次方程,而是一元一次方程,也有唯一解,所以本题要分三种情况讨论 .
[解]
当x2-2≠0时,x+a=x2+a
⊿=0 a=-
a=-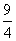 ,此时,x=
,此时,x=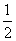 ,符合题意,
,符合题意,
当a=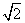 时,x=
时,x=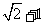 ,符合题意,
,符合题意,
当a=-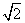 时,x=
时,x= ,也符合题意,
,也符合题意,
∴ A={ ,
,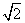 ,-
,-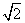 }
}
[师生互动]
|
学生质疑 |
|
|
教师释疑 |
|
例4.已知集合P={-1,a,b},Q={-1,a2,b2},且Q=P,求1+a2+b2的值.
分析:含字母的两个集合相等,并不意味着 按序对应相等,要分类讨论,同时也要考虑集合中的元素的互异性和无序性.
[解]
分两种情况讨论:①
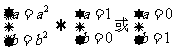
 1+a2+b2=2
1+a2+b2=2
②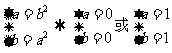 这与集合的性质矛盾,
这与集合的性质矛盾,
∴ 1+a2+b2=2
追踪训练
1.集合A={x|y=x2+1},B={t|p=t2+1}
C={y|x =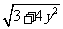 },这三个集合
},这三个集合
的关系?
3. 下列集合表示法正确的是
(1) {1,2,2};
(2) {Ф};
(3) {全体有理数};
(4) 方程组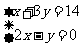 的解的集合为
的解的集合为
{2,4};
(5)不等式x2-5>0的解集为{x2-5>0}.
例3.已知A={a|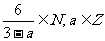 },
},
试用列举法表示集合A.
分析:用列举法表示的集合,要认清集合的实质,集合中的元素究竟满足哪

 些条件.
些条件.
[解]
当a=2时,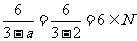
当a=1时,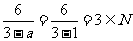
当a=0时,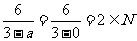
当a=-1时,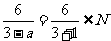
当a=-2时,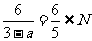
当a=-3时,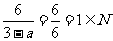
∴ A={2,1,0,-3}
点评:本题实际上是要求满足6被3-a整除的
整数a的值,若将题目改为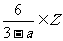 ,
,
则集合A={-3,0,1,2,4,5,6,9}.
2. 用描述法表示下列集合:
(1) 奇数的集合;
(2)正偶数的集合;
(3)不等式2x-3>5的解集;
(4)直角坐标平面内属于第四象限的点的
集合; .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com