
例1、下列集合M到P的对应f是映射的是( )
A.M={-2,0,2},P={-1,0,4},f:M中数的平方
B.M={0,1},P={-1,0,1},f:M中数的平方根
C.M=Z,P=Q,f:M中数的倒数。
D.M=R,P=R+,f:M中数的平方
[解]:
判定对应f:A→B是否是映射,关键是看是否符合映射的定义,即集合A中的每一个元素在B中是否有象且唯一,若不是映射只要举一反例即可。
答案:选择A
5、函数f(x)=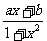 是定义在(-1,1)上的奇函数,且f(
是定义在(-1,1)上的奇函数,且f(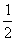 )=
)=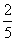 .
.
(1)确定函数f(x)的解析式;
(2)用定义证明f(x)在(-1,1)上是增函数;
(3)解不等式f(t-1)+f(t)<0;
答案:(1)f(x)=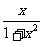
(2)证明略
(3)0<t<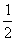
4、已知f(x)是偶函数,g(x)是奇函数,它们的定义域均为{x|x∈R且x≠±1},若f(x)+g(x)=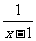 ,则f(x)=________,g(x)=__________
,则f(x)=________,g(x)=__________
答案:f(x)=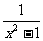 ,g(x)=
,g(x)=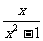
.
3、设f(x)在R上是偶函数,在区间(-∞,0)上递增,且有f(2a2+a+1)<f(3a2-2a+1),求a的取值范围。
答案:0<a<3
2、下列函数中,在区间(-∞,0)上为增函数的是( )
A.y=1+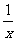 B.y=-(x+1)2
B.y=-(x+1)2
C.y=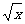 D.y=x3
D.y=x3
答案:D
例4、设f(x)是定义在[-2,2]上的偶函数,当x≥0时,f(x)单调递减,若f(1-m)<f(m)成立,求m的取值范围。
思维分析:要求m的取值范围,就要列关于m的不等式,由f(1-m)<f(m)且f(x)是偶函数知1-m与m的符号不能确定,由偶函数的性质可按1-m与m同号;1-m与m异号两种情况,列四个不等式组,计算非常繁琐,但考虑到偶函数f(x)=f(|x|),可将问题转化为只考虑x>0时的情况,从而使问题简单化。
解:因为函数f(x)在[-2,2]上是偶函数,则由f(1-m)<f(m)可得f(|1-m|)<f(|m|).
又x≥0时,f(x)是单调减函数,
所以 。
。
解之得:-1≤m<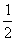 .
.
追踪训练
1、函数f(x)=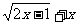 的值域是( )
的值域是( )
A.[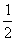 ,+∞) B.(-∞,
,+∞) B.(-∞,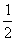 ]
]
C.(0,+∞) D.[1,+ ∞)
答案:A
例3、已知y=f(x)是偶函数,且图象与x轴四个交点,则方程f(x)=0的所有实根之和是( )
A.4 B.2 C.0
D.不知解析式不能确定
思维分析:因为f(x)是偶函数且图象与x轴有四个交点,这四个交点每两个关于原点一定是对称的,故x1+x2+x3+x4=0.
答案:C
例2、求函数y= 的单调区间,并对其中一种情况证明。
的单调区间,并对其中一种情况证明。
思维分析:要求出y= 的单调区间,首先求出定义域,然后利用复合函数的判定方法判断.
的单调区间,首先求出定义域,然后利用复合函数的判定方法判断.
解:设u=x2-2x-3,则y=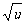 .
.
因为u≥0,所以x2-2x-3≥0.所以x≥3或x≤-1.
因为y=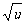 在u≥0时是增函数,又当x≥3时,u是增函数,
在u≥0时是增函数,又当x≥3时,u是增函数,
所以当x≥3时,y是x的增函数。
又当 x≤-1时,u是减函数,
所以当x≤-1时,y是x的减函数。
所以y= 的单调递增区间是[3,+ ∞),单调递减区间是(-∞,-1]。
的单调递增区间是[3,+ ∞),单调递减区间是(-∞,-1]。
证明略
例1、已知函数y=f(x)对任意x,y∈R均为f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,f(1)= -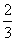 .
.
(1)判断并证明f(x)在R上的单调性;
(2)求f(x)在[-3,3]上的最大、小值。
思维分析:抽象函数的性质要紧扣定义,并同时注意特殊值的应用。
解:(1)令x=y=0,f(0)=0,令x=-y可得:
f(-x)= -f(x),在R上任取x1<x2,
则x2-x1>0,
所以f(x2) -f(x1)=f(x2)+f(-x1)=f(x2-x1).
因为x1<x2,所以x2-x1>0。
又因为x>0时f(x)<0,
所以f(x2-x1)<0,即f(x2)<f(x1).
由定义可知f(x)在R上是减函数.
(2)因为f(x)在R上是减函数,
所以f(x)在[-3,3]上也是减函数.
所以f(-3)最大,f(3)最小。
所以f(-3)= -f(3)=2
即f(x)在[-3,3]上最大值为2,最小值为-2。
5.定义在实数集上的函数f(x),对任意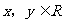 ,有
,有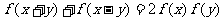 且
且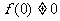 。
。
(1)求证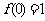 ;(2)求证:
;(2)求证: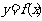 是偶函数。
是偶函数。
解(1)令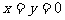 ,则有
,则有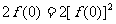
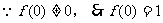
(2)令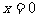 ,则有
,则有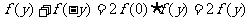
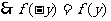 这说明
这说明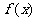 是偶函数
是偶函数
|
学生质疑 |
|
|
教师释疑 |
|
 [师生互动]
[师生互动]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com