
3. 函数f(x+1)=x2-2x+1的定义域是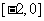 ,则f(x)的单调递减区间是__
,则f(x)的单调递减区间是__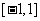 ______.
______.
2. 若函数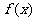 是
是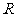 上的增函数,对于实数
上的增函数,对于实数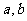 ,若
,若 ,则有(A )
,则有(A )
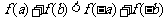
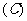
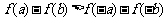
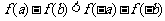
我们只要画出函数的草图,在草图上要能够反映函数图像的上升和下降,根据图像上升的区间就是函数的单调增区间,图像下降的区间就是函数的单调减区间.
追踪训练
1.函数y=3x-2x2+1的单调递增区间是
(B )
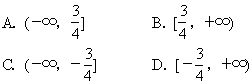
2.单调区间是单调增区间和单调减区间的统称,所以,求函数的单调区间时,如果函数既有单调增区间,又有单调减区间,必须分别写出来。
思维点拔:
1.单调区间是函数定义域的子集,所以,求函数的单调区间,必须注意函数的定义域;
3. 求证: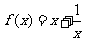 在区间
在区间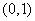 上是减函数.
上是减函数.
证明:设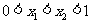 ,则
,则
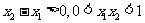
∴

即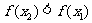
故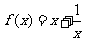 在区间
在区间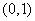 上是减函数.
上是减函数.

[选修延伸]
如果一个函数有两个单调区间,两个区间一般不取并集:
例3: 函数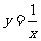 在其定义域
在其定义域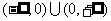 上是减函数吗?
上是减函数吗?
分析:单调区间的判断目前只有通过定义进行说明,如果要说明这个命题是真命题时我们要给出严格的定义证明,而如果要说明这个命题是假命题,我们只要举一组不满足定义的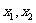 ,并加以说明.
,并加以说明.
[解]
该命题是假命题;例如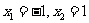 时,
时, 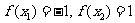 ,显然
,显然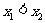 且
且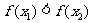 ,所以"函数
,所以"函数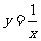 在其定义域
在其定义域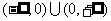 上是减函数"是不成立的.
上是减函数"是不成立的.
点评:
2. 函数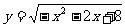 的单调增区间为
的单调增区间为 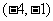 ..
..
例2:求证:函数f(x)= -x3+1在区间(-∞,+ ∞)上是单调减函数
证明:设x1,x2∈R且x1<x2,则f(x1) -f(x2)= -x13+1+x23-1
=(x2-x1)(x22+x1x2+x12)
因为x2>x1,x22+x1x2+x12>0
所以f(x1) -f(x2)>0即
f(x1)>f(x2)
所以f(x)在(-∞,+ ∞)上递减
追踪训练一
1. 函数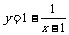 (C)
(C)
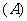 在
在 内单调递增
内单调递增
 在
在 内单调递减
内单调递减
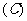 在
在 内单调递增
内单调递增
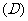 在
在 内单调递减
内单调递减
例1:画出下列函数图象,并写出单调区间.
(1) ;
;
(2)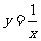 ;
;
(3)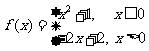 .
.
[解]
(图略)
(1)函数 的单调增区间为
的单调增区间为 ,单调减区间为
,单调减区间为 ;
;
(2)函数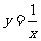 在
在 和
和 上分别单调减,即其有两个单调减区间分别是
上分别单调减,即其有两个单调减区间分别是 和
和 .
.
(3)函数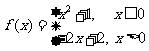 在实数集
在实数集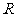 上是减函数;
上是减函数;
2.函数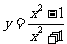 的值域是
的值域是 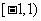 。
。
|
学生质疑 |
|
|
教师释疑 |
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com