1: (2002年高考上海文，理16)一般地，家庭用电量(千瓦时)与气温(℃)有一定的关系，如图所示，图(1)表示某年个月中每月的平均气温.图(2)表示某家庭在这年个月中每个月的用电量.根据这些信息，以下关于该家庭用电量与其气温间关系的叙述中，正确的是(　　 )

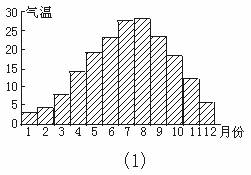
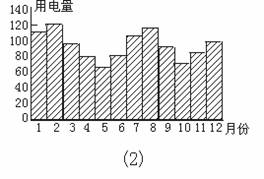
A.气温最高时，用电量最多

B.气温最低时，用电量最少

C.当气温大于某一值时，用电量随气温增高而增加

D.当气温小于某一值时，用电量随气温渐低而增加

思维点拔：

数学应用题的一般求解程序

(1)审题：弄清题目意，分清条件和结论，理顺数量关系；

(2)建模：将题目条件的文字语言转化成数学语言，用数学知识建立相应的数学模型；

(3)解模：求解数学模型，得到数学结论；

(4)结论：将用数学方法得到的结论还原为实际问题的意义，并根据题意下结论．

追踪训练二

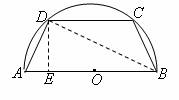
1. 有一块半径为的半圆形钢板，计划剪裁成等腰梯形的形状，它的下底是⊙O的直径，上底的端点在圆周上，写出这个梯形周长和腰长间的函数关系式，并求出它的定义域．

8．判断方程(其中)在区间内是否有解．

[解]

7．求方程的近似解(精确到)．

[解]

6．已知函数过点，则方程的解为　　 　　　．

5．已知方程在区间中有且只有一解，则实数的取值范围为　　　　　　　　　 .

4．函数与轴交点坐标是　　　 ，方程的根为　　　　　　 ．

3．直线与曲线只有一个公共点，则k的值为　　　　　　　　　　　　 (　　 )

A. 0，　　　 　　　 B. 0，　　　

C. 　　　　　　　D. 0，

2．已知则方程的解的个数是(　　 )　

A.　　　 B. 　　　C.　　 D. 不确定

1．函数的图象与轴交点横坐标为　　 (　 )

)

A.　　　 B. 　　C.或　　 　D.

3．二分法求方程的近似解

　　 二分法求方程的近似解，首先要找到方程的根所在的区间，则必有，再取区间的中点，再判断的正负号，若，则根在区间中；若，则根在中；若，则即为方程的根．按照以上方法重复进行下去，直到区间的两个端点的近似值相同(且都符合精确度要求)，即可得一个近似值．

[精典范例]

例1：已知二次函数的图象经过点三点，

(1)求的解析式；

(2)求的零点；

(3)比较，，，与的大小关系．

[解]

例2：利用计算器，求方程的近似解(精确到)．

[解]

例3：已知函数的图象与轴在原点的右侧有交点，试确定实数的取值范围．

[解]

追踪训练一