5．定义在实数集上的函数f(x)，对任意，有且。

(1)求证；(2)求证：是偶函数。

解(1)令，则有

　 (2)令，则有

　 这说明是偶函数

[师生互动]

3. 是奇函数，它在区间(其中)上为增函数，则它在区间上(D)

　　 A. 是减函数且有最大值

　　 B. 是减函数且有最小值

　　 C. 是增函数且有最小值

　　 D. 是增函数且有最大值

4已知函数，且，则　 　　．

2. 已知偶函数在上是增函数，若，则必有( C )

　　若函数是偶函数，则该函数在关于＂0＂对称的区间上的单调性是相反的，且一般情况下偶函数在定义域上不是单调函数；若函数是奇函数，则该函数在关于＂0＂对称区间上的点调性是相同的．

追踪训练

1．已知是偶函数，其图象与轴共有四个交点，则方程的所有实数解的和是　 　　　　　 (C)

　 4　 　2　 0　　 不能确定

3. 　函数是定义在上的奇函数，且为增函数，若，求实数a的范围。

解：定义域是

即

　　 又

　　 是奇函数

　　 在上是增函数

即

　　 解之得　

　　 故a的取值范围是

思维点拔：

2. 定义在上的奇函数，则常数　 0　　 ，　　 0　　 ；

例2：已知是定义域为的奇函数，当时，，求的解析式，并写出的单调区间．

[解]设，则，由已知得，

　　 ∵是奇函数，∴，

　　 ∴当时，；

　　 又是定义域为的奇函数，∴．

　 综上所述：

　 的单调增区间为，单调增区间为和．

说明：一般情况下，若要求在区间上的解析式，就在区间上设．

例3：定义在上的奇函数在整个定义域上是减函数，若，

求实数的取值范围．

[解]原不等式化为，

∵是奇函数，∴，

∴原不等式化为，

∵是减函数，∴，

∴．　　　　 ①

又的定义域为，

∴，解得，②

由①和②得实数的取值范围为．

追踪训练一

1. 设是定义在R上的偶函数,且在上是增函数,则与

()的大小关系是　 (B　 )

　　　 A．<　　　　　　　　　

B．≥

　　　 C．>

　　　 D．与a的取值无关

例1：已知奇函数在上是增函数，求证：在上也是增函数．

[证明]

设，则，∵在上是增函数，

∴，∵是奇函数，∴，，

∴，∴，∴在上也是增函数．

说明：一般情况下，若要证在区间上单调，就在区间上设．

5．若是定义在上的函数，是奇函数，是偶函数，且，求的表达式．

[师生互动]

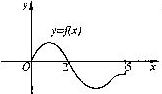
4. 设奇函数f(x)的定义域为[－5,5].

若当x∈[0,5]时, 　f(x)的图象如下图,则

不等式的解是　 　　　 .