
6. 抛物线y2=2x上到直线x-y+3=0距离最短的点的坐标为__________
抛物线y2=2x上到直线x-y+3=0距离最短的点的坐标为__________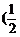 ,1)
,1)
5.设F是椭圆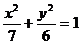 的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为____
的右焦点,且椭圆上至少有21个不同的点Pi(i=1,2,3,…),使|FP1|,|FP2|,|FP3|,…组成公差为d的等差数列,则d的取值范围为____
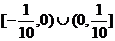 .
.
4.已知点P是抛物线y2=4x上一点,设P到此抛物线的准线的距离为d1, 到直线x+2y+10=0的距离为d2,则d1+d2的最小值为 ( C )
A.5 B.4 C.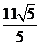 (D)
(D)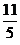
3.已知双曲线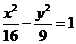 ,过其右焦点F的直线l交双曲线于AB,若|AB|=5,则直线l有( B )
,过其右焦点F的直线l交双曲线于AB,若|AB|=5,则直线l有( B )
A.1条 B.2条 C.3条 D.4条
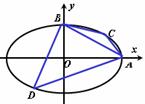
2.已知A(3,2)、B(-4,0),P是椭圆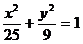 上一点,则|PA|+|PB|的最大值为( C
)
上一点,则|PA|+|PB|的最大值为( C
)
A.10 B.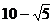 C.
C.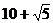 D.
D.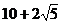
1.设AB是过椭圆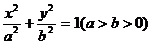 中心的弦,椭圆的左焦点为F1(-c,0),则△F1AB的面积最大为( A
)
中心的弦,椭圆的左焦点为F1(-c,0),则△F1AB的面积最大为( A
)
A.bc B.ab C.ac D.b2
2.函数法是我们探求解析几何最值问题的首选方法,其中所涉及到的函数最常见的有二次函数等,值得注意的是函数自变量取值范围的考察不能被忽视。
[文]设P是椭圆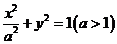 短轴的一个端点,Q为椭圆上的一个动点,求|PQ|的最大值。
短轴的一个端点,Q为椭圆上的一个动点,求|PQ|的最大值。
解: 依题意可设P(0,1), Q(x,y),则 |PQ|=,又因为Q在椭圆上,
所以x2=a2(1-y2) , |PQ|2= a2(1-y2)+y2-2y+1=(1-a2)y2-2y+1+a2
=(1-a2)(y- )2-+1+a2 .
因为|y|≤1,a>1, 若a≥, 则||≤1, 当y=时, |PQ|取最大值;
若1<a<,则当y=-1时, |PQ|取最大值2.
[范例4]已知△OFQ的面积为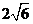 ,
,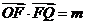
(1)设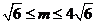 ,求ÐOFQ正切值的取值范围;
,求ÐOFQ正切值的取值范围;
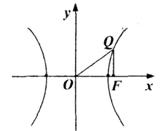 (2)设以O为中心,F为焦点的双曲线经过点Q(如图),
(2)设以O为中心,F为焦点的双曲线经过点Q(如图),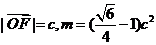 当
当 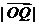 取得最小值时,求此双曲线的方程。
取得最小值时,求此双曲线的方程。
解析:(1)设ÐOFQ =q
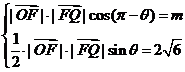
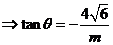
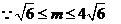
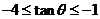
(2)设所求的双曲线方程为
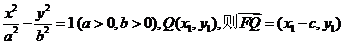
∴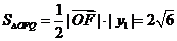 ,∴
,∴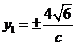
又∵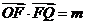 ,∴
,∴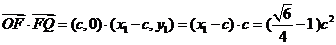
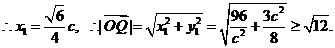
当且仅当c=4时,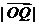 最小,此时Q的坐标是
最小,此时Q的坐标是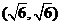 或
或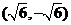
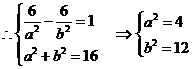 ,所求方程为
,所求方程为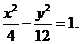
[点晴]当题中的条件和结论体现出一种明显的函数关系时,可通过建立目标函数,求其目标函数的最值,求函数最值的常用方法有:一元二次函数法、基本不等式法、判别式法、定义法、函数单调性法等。
[文]已知椭圆的一个焦点为F1(0,-2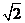 ),对应的准线方程为
),对应的准线方程为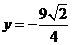 ,且离心率e满足:
,且离心率e满足: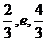 成等差数列。
成等差数列。
(1)求椭圆方程;
(2)是否存在直线l,使l与椭圆交于不同的两点M、N,且线段MN恰被直线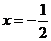 平分,若存在,求出l的倾斜角的范围;若不存在,请说明理由。
平分,若存在,求出l的倾斜角的范围;若不存在,请说明理由。
(1)解:依题意e 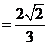 ,
,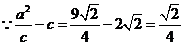
∴a=3,c=2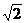 ,b=1,
,b=1,
又F1(0,-2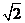 ),对应的准线方程为
),对应的准线方程为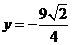
∴椭圆中心在原点,所求方程为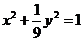
(2)假设存在直线l,依题意l交椭圆所得弦MN被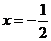 平分
平分
∴直线l的斜率存在。 设直线l:y=kx+m
由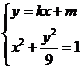 消去y,整理得 (k2+9)x2+2kmx+m2-9=0
消去y,整理得 (k2+9)x2+2kmx+m2-9=0
∵l与椭圆交于不同的两点M、N,
∴Δ=4k2m2-4(k2+9)(m2-9)>0 即m2-k2-9<0 ①
设 M(x1,y1),N(x2,y2) 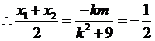
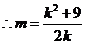 ②
②
把②代入①式中得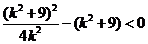
∴k>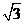 或k<-
或k<-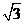
∴直线l倾斜角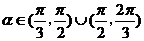
★★★自我提升
6.设椭圆方程为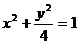 ,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足
,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足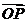
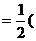
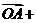
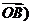 ,点N的坐标为
,点N的坐标为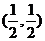 ,当l绕点M旋转时,求(1)动点P的轨迹方程;(2)
,当l绕点M旋转时,求(1)动点P的轨迹方程;(2)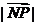 的最小值与最大值.
的最小值与最大值.
[专家解答](1)法1:直线l过点M(0,1)设其斜率为k,则l的方程为y=kx+1.
|
|
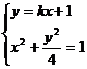 的解.
将①代入②并化简得(4+k2)x2+2kx-3=0,
的解.
将①代入②并化简得(4+k2)x2+2kx-3=0,
所以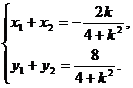
于是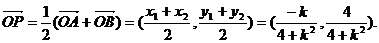
设点P的坐标为(x,y), 则
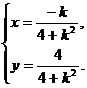 消去参数k得4x2+y2-y=0 ③
消去参数k得4x2+y2-y=0 ③
当k不存在时,A、B中点为坐标原点(0,0),也满足方程③,
所以点P的轨迹方程为4x2+y2-y=0
解法二:设点P的坐标为(x,y),因A(x1,y1),B(x2,y2)在椭圆上,所以
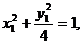 ④
④
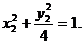 ⑤
⑤
④-⑤得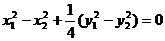 ,
,
所以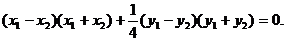
当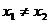 时,有
时,有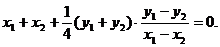 ⑥
⑥
并且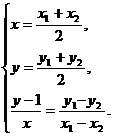 ⑦ 将⑦代入⑥并整理得 4x2+y2-y=0 ⑧
⑦ 将⑦代入⑥并整理得 4x2+y2-y=0 ⑧
当x1=x2时,点A、B的坐标为(0,2)、(0,-2),这时点P的坐标为
(0,0)也满足⑧,所以点P的轨迹方程为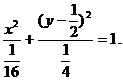
(2)由点P的轨迹方程知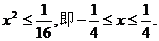 所以
所以
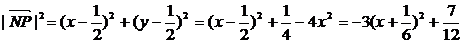
故当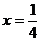 ,
,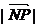 取得最小值,最小值为
取得最小值,最小值为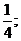
当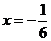 时,
时,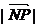 取得最大值,最大值为
取得最大值,最大值为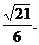
★★★高考要考什么
[考点透视]
与圆锥曲线有关的最值和范围问题,因其考查的知识容量大、分析能力要求高、区分度高而成为高考命题者青睐的一个热点。
[热点透析]
与圆锥曲线有关的最值和范围问题的讨论常用以下方法解决:
(1)结合定义利用图形中几何量之间的大小关系;
(2)不等式(组)求解法:利用题意结合图形(如点在曲线内等)列出所讨论的参数适合的不等式(组),通过解不等式组得出参数的变化范围;
(3)函数值域求解法:把所讨论的参数作为一个函数、一个适当的参数作为自变量来表示这个函数,通过讨论函数的值域来求参数的变化范围。
(4)利用代数基本不等式。代数基本不等式的应用,往往需要创造条件,并进行巧妙的构思;
(5)结合参数方程,利用三角函数的有界性。直线、圆或椭圆的参数方程,它们的一个共同特点是均含有三角式。因此,它们的应用价值在于:
① 通过参数θ简明地表示曲线上点的坐标;
② 利用三角函数的有界性及其变形公式来帮助求解诸如最值、范围等问题;
(6)构造一个二次方程,利用判别式D³0。
★★★突破重难点
[范例1]已知动点P与双曲线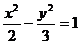 的两个焦点F1、F2的距离之和为定值,且cosÐF1PF2的最小值为
的两个焦点F1、F2的距离之和为定值,且cosÐF1PF2的最小值为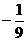 .
.
(1)求动点P的轨迹方程;
(2)若已知D(0,3),M、N在动点P的轨迹上且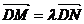 ,求实数l的取值范围.
,求实数l的取值范围.
讲解 (1)由题意c2=5.设|PF1|+|PF2|=2a(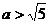 ),由余弦定理, 得
),由余弦定理, 得
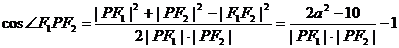 .
.
又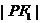 ·
·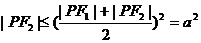 ,
,
当且仅当|PF1|=|PF2|时,|PF1|·|PF2| 取最大值,
此时cosÐF1PF2取最小值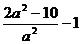 ,令
,令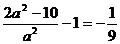 ,
,
解得a2=9,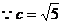 ,∴b2=4,故所求P的轨迹方程为
,∴b2=4,故所求P的轨迹方程为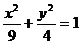 .
.
(2)设N(s,t),M(x,y),则由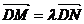 ,可得(x,y-3) =l(s,t-3),
,可得(x,y-3) =l(s,t-3),
故x=ls,y=3+l(t-3).
∵M、N在动点P的轨迹上,
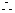
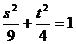 且
且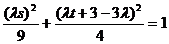 ,
,
消去s可得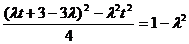 ,解得
,解得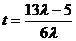 ,
,
又|t|£2,∴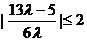 ,解得
,解得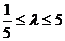 ,
,
故实数l的取值范围是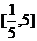 .
.
[点晴]为了求参数的取值范围,只要列出关于参数的不等式,而建立不等式的方法有多种方法,诸如:判别式法、均值不等式法、有界性法等等.
[文]已知点M(-2,0),N(2,0),动点P满足条件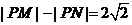 .记动点
.记动点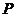 的轨迹为W.
的轨迹为W.
(Ⅰ)求W的方程;
(Ⅱ)若A,B是W上的不同两点,O是坐标原点,求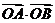 的最小值.
的最小值.
解:(Ⅰ)依题意,点P的轨迹是以M,N为焦点的双曲线的右支,
所求方程为: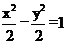 (x>0)
(x>0)
(Ⅱ)当直线AB的斜率不存在时,设直线AB的方程为x=x0,
此时A(x0,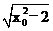 ),B(x0,-
),B(x0,-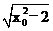 ),
),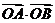 =2
=2
当直线AB的斜率存在时,设直线AB的方程为y=kx+b,
代入双曲线方程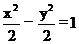 中,得:(1-k2)x2-2kbx-b2-2=0
中,得:(1-k2)x2-2kbx-b2-2=0
依题意可知方程1°有两个不相等的正数根,设A(x1,y1),B(x2,y2),则
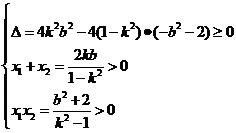 解得|k|>1,
解得|k|>1,
又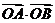 =x1x2+y1y2=x1x2+(kx1+b)(kx2+b)
=x1x2+y1y2=x1x2+(kx1+b)(kx2+b)
=(1+k2)x1x2+kb(x1+x2)+b2=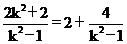 >2
>2
综上可知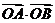 的最小值为2
的最小值为2
[范例2]给定点A(-2,2),已知B是椭圆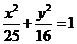 上的动点,F是右焦点,当
上的动点,F是右焦点,当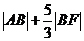 取得最小值时,试求B点的坐标。
取得最小值时,试求B点的坐标。
解析:因为椭圆的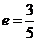 ,所以
,所以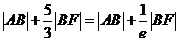 ,而
,而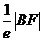 为动点B到左准线的距离。故本题可化为,在椭圆上求一点B,使得它到A点和左准线的距离之和最小,过点B作l的垂线,垂点为N,过A作此准线的垂线,垂点为M,由椭圆定义
为动点B到左准线的距离。故本题可化为,在椭圆上求一点B,使得它到A点和左准线的距离之和最小,过点B作l的垂线,垂点为N,过A作此准线的垂线,垂点为M,由椭圆定义
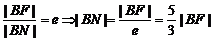
于是 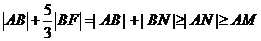 为定值
为定值
其中,当且仅当B点AM与椭圆的定点时等点成立,此时B为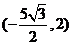
所以,当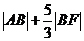 取得最小值时,B点坐标为
取得最小值时,B点坐标为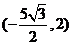
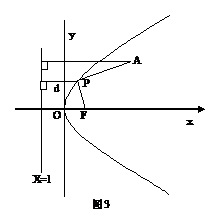 [点晴]在处理许多与焦点有关的距离和差最值问题时,常常用圆锥曲线的定义化折为直,是一种简便而有效的好方法。
[点晴]在处理许多与焦点有关的距离和差最值问题时,常常用圆锥曲线的定义化折为直,是一种简便而有效的好方法。
[文]点A(3,2)为定点,点F是抛物线y2=4x
的焦点,点P在抛物线y2=4x上移动,若|PA|+|PF|
取得最小值,求点P的坐标。
解:抛物线y2=4x的准线方程为x=-1,
设P到准线的距离为d,则|PA|+|PF|=|PA|+d。
要使|PA|+|PF|取得最小值,由图3可知过A点
的直线与准线垂直时,|PA|+|PF|取得最小值,把y=2
代入y2=4x,得P(1,2)。
[范例3]已知P点在圆x2+(y-2)2=1上移动,Q点在椭圆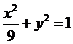 上移动,试求|PQ|的最大值。
上移动,试求|PQ|的最大值。
解:故先让Q点在椭圆上固定,显然当PQ通过圆心O1时|PQ|最大,因此要求|PQ|的最大值,只要求|O1Q|的最大值.设Q(x,y),则|O1Q|2= x2+(y-4)2 ①
因Q在椭圆上,则x2=9(1-y2) ②
将②代入①得|O1Q|2=
9(1-y2)+(y-4)2 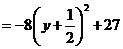
因为Q在椭圆上移动,所以-1£y£1,故当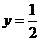 时,
时,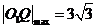
此时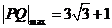
[点晴]1.与圆有关的最值问题往往与圆心有关;
5.已知抛物线y2=4x,过点P(4,0)的直线与抛物线相交于A(x1,y1),B(x2,y2)两点,则y12+y22的最小值是 32 .
4.已知双曲线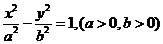 的左、右焦点分别为F1、F2,点P在双曲线的右支上,且|PF1|=4|PF2|,则此双曲线的离心率e的最大值为:(B)
的左、右焦点分别为F1、F2,点P在双曲线的右支上,且|PF1|=4|PF2|,则此双曲线的离心率e的最大值为:(B)
(A)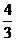 (B)
(B)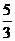 (C)
(C)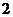 (D)
(D)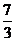
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com