
所以
 ,令
,令 =
= ,
, ,
,

 ,所以0<
,所以0<
对任意的 ,
, ,
,
解:(I)对任意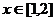 ,
, ,
,
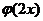
 ,
, ,所以
,所以 ,
,
(III) 设 ,任取
,任取 ,令
,令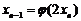 ,
, ,证明:给定正整数
,证明:给定正整数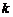 ,对任意的正整数
,对任意的正整数 ,成立不等式
,成立不等式
(II)设 ,如果存在
,如果存在 ,使得
,使得 ,那么这样的
,那么这样的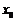 是唯一的;
是唯一的;
(I)设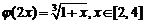 ,证明:
,证明:
55.(广东卷)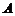 是定义在
是定义在 上且满足如下条件的函数
上且满足如下条件的函数 组成的集合:①对任意的
组成的集合:①对任意的 ,都有
,都有 ;②存在常数
;②存在常数 ,使得对任意的
,使得对任意的 ,都有
,都有 .
.
解:先求原函数的值域,再反解.由y=3x+5,x∈[0,1] ,得y∈[5,8] .解出  ,从而
,从而  ,x∈[5,8]
. 从而应填
,x∈[5,8]
. 从而应填  .
.
54.(上海春)已知函数 是定义在
是定义在 上的偶函数. 当
上的偶函数. 当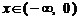 时,
时, ,则 当
,则 当 时,
时, .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com