
2009最有影响力高考复习题(数学)7(3+3+4)
文博浪花工作室王培博推荐(
一、选择题:
1、以下函数f (x),具有性质(x-1) f ¢(x)≥0从而有f (0)+ f (2) ≥
A. f(x)= (x-1)3 B. f(x)= (x-1)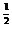 C. f(x)= (x-1)
C. f(x)= (x-1)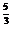 D. f(x)= (x-1)
D. f(x)= (x-1)
2、过正三棱锥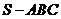 侧棱
侧棱 与底面中心
与底面中心 作截面
作截面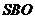 ,已知截面是等腰三角形,则侧面和底面所成角的余弦值为 ( )
,已知截面是等腰三角形,则侧面和底面所成角的余弦值为 ( )
A.  B.
B.
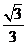 C.
C.
 或
或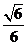 D.
D. 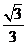 或
或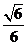
3、已知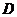 为
为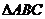 的边
的边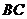 的中点,
的中点,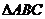 所在平面内有一点
所在平面内有一点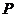 ,满足
,满足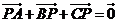 ,设
,设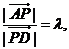 则
则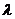 的值为( )
的值为( )
A. 2
B. 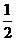 D.
D.
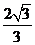
二、填空题:
5、设函数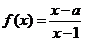 ,集合M=
,集合M=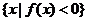 ,P=
,P=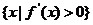 ,若M
,若M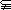 P,则实数a的取值范围是
P,则实数a的取值范围是

.6、已知M是椭圆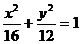 上的动点,椭圆内有一定点A(-2,
上的动点,椭圆内有一定点A(-2,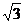 ), F是椭圆的右焦点,试求|MA|+2|MF|的最小值,则点M的坐标 。答(2
), F是椭圆的右焦点,试求|MA|+2|MF|的最小值,则点M的坐标 。答(2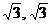 )
)
三、解答题:
7.矩形ABCD中,AB=6,BC=2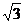 ,沿对角线BD将△ABD向上折起,使点A移到点P,并使点P在平面BCD上的射影O在DC上(如图所示).?
,沿对角线BD将△ABD向上折起,使点A移到点P,并使点P在平面BCD上的射影O在DC上(如图所示).?
?8、某商场为了促销,当顾客购买商品的金额达到一定数量之后可通过抽奖的方法获奖,箱中有4只红球和3只白球,当抽到红球时奖励20元的商品,当抽到白球时奖励10元的商品(当顾客通过抽奖的方法确定了获奖商品后,即将小球全部放回箱中).?
(1)当顾客购买金额超过500元而少于1000元时,可抽取3个小球,求其中至少有一个红球的概率;?
(2)当顾客购买金额超过1000元时,可抽取4个小球,设他所获奖商品的金额为ξ(ξ=50,60
,70,80)元,求ξ的概率分布和期望
9、已知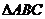 中,A,B,C的对边分别为
中,A,B,C的对边分别为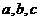 ,且()2=?+?+?.
,且()2=?+?+?.
(Ⅰ)判断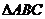 的形状,并求
的形状,并求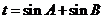 的取值范围;
的取值范围;
(Ⅱ)若不等式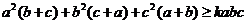 ,对任意的满足题意的
,对任意的满足题意的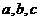 都成立,求
都成立,求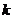 的取值范围.
的取值范围.
1、【解答】 对A,f (0)= -1, f (2) =1,f (1)=0,不符合要求;对B,f (0)无意义;
对C,f (0)= -1, f (2) =1,f (1)=0,不符合要求;答案只能是D. 对D, f (0)= 1, f (1) =0,f (2)=1.
且f ¢(x)=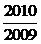 (x-1)
(x-1)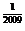 使得 (x-1) f'(x) =(x-1)
使得 (x-1) f'(x) =(x-1)
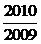 (x-1)
(x-1)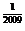 ≥0.
≥0.
[说明] 以x=1为对称轴、开口向上的函数都属这类抽象函数. 如f¢(x)=(x-1) 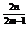 ,其中m,n都是正整数,且n≥m.
,其中m,n都是正整数,且n≥m.
2、【解答】C 3、【解答】A
4、【解答】如图所示,令A1P = CQ = 0. 即动点P与A1重合,动点Q与C重合.
显然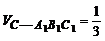 V棱柱.∴
V棱柱.∴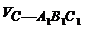 ∶
∶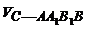 =
=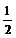
5、【解答】设函数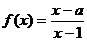 , 集合
, 集合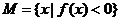 .
.
若a>1时,M={x| 1<x<a};
若a<1时,M={x| a<x<1};
若a=1时,M=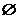 .
.
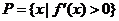 ,∴
,∴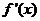 =
= >0.
>0.
∴ a>1时,P=R,a<1时,P=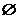 ;已知
;已知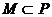 ,所以 (1,+∞).
,所以 (1,+∞).
作MB垂直于右准线l,垂足为B,如图所示.则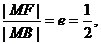
即|MB|=2|MF|, 所以|MA|+2|MF|=|MA|+|MB|.
易知点M在线段AB上时,|MA|+2|MF|取最小值8,这时点M的坐标?为(2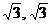 ).
).
7、分析 (1)为证PD⊥PC,须先证PD⊥平面PBC,已有PD⊥PB(翻折前为AD⊥AB),还须PD⊥BC.?
(2)求二面角的要点是找出二面角的平面角,已有PO⊥平面BCD于O,且?O∈CD?,只须作OM⊥BD?即可.??
【解答】 (1)由条件知PO⊥平面BCD于O,且?O∈CD,?BC⊥CD,∴BC⊥PD(三垂线定理),但PD⊥PB,∴PD⊥面PBC,从而PD⊥PC.?
(2)作OM⊥BD于M,连接PM,则BD⊥PM(三垂线定理),∴∠PMO是二面角P―BD―C的平面角,?
∵PB=6, PD=2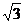 ,∴BD=4
,∴BD=4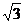 ,PM=
,PM=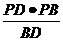 =3,?
=3,?
已证PD⊥PC,∴PC= ,PO=
,PO=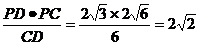 .?
.?
?sin∠PMO=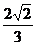 ,∠PMO=arcsin
,∠PMO=arcsin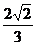 ,?即所求二面角P―DB―C的大小为?arcsin
,?即所求二面角P―DB―C的大小为?arcsin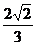 .?
.?
8、【解答】 (1)基本事件总数n=C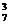 =35, 设事件A={任取3球,至少有一个红球},则事件?
=35, 设事件A={任取3球,至少有一个红球},则事件?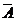 ={任取3球,全是白球}.?
={任取3球,全是白球}.?
∵A与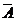 为对立事件,而Card
为对立事件,而Card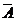 =1(任取3球全是白球仅一种可能).?
=1(任取3球全是白球仅一种可能).?
∴P(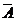 )=
)=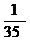 ,于是P (A)=1-P (
,于是P (A)=1-P (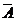 )=
)=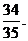 即该顾客任取3球,至少有一个红球的概率为
即该顾客任取3球,至少有一个红球的概率为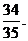
(2)ξ=50表示所取4球为3白1红(∵3×10+1×20=50),?∴P (ξ=50)=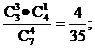
ξ=60表示所取4球为2白2红(∵2×10+2×20=60), ∴P (ξ=60)= 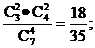 ??
??
ξ=70表示所取4球为3红1白(∵3×20+1×10=70), ∴P (ξ=70)= 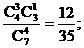
ξ=80表示所取4球全为红球, ∴P (ξ=80)= 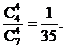
于是ξ的分布列为:?
ξ
50
60
70
80
P
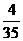
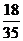
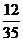
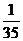
∴Dξ=50×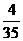 +60×
+60×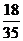 +70×
+70×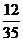 +80×
+80×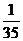 =
=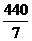 (元).?即该顾客获奖的期望是
(元).?即该顾客获奖的期望是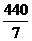 ≈63(元).??
≈63(元).??
9、【解答】(Ⅰ)∵()2=?+?+?,∴ ()2=?(+)+? ,
即()2=?+?,即?=0.∴△ABC 是以C为直角顶点的直角三角形.
∴sinA+sinB=sinA+cosA=sin(A+),A∈(0,) ,
∴sinA+sinB的取值范围为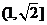 .
.
(Ⅱ)在直角△ABC中, a=csinA,b=ccosA.
若a2(b+c)+b2(c+a)+c2(a+b)≥kabc,对任意的满足题意的a、b、c都成立,
则有≥k,对任意的满足题意的a、b、c都成立,
∵
=[c2sin2A(ccosA+c)+c2cos2A(csinA+c)+c2(csinA+ccosA)]
=[ sin2AcosA+cos2A sinA+1+cosA+sinA]=cosA+sinA+
令t=sinA+cosA,t∈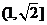 ,
,
设f(t)==t+=t+=t-1++1.
f(t)=t-1++1,当t-1∈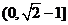 时 f(t)为单调递减函数,
时 f(t)为单调递减函数,
∴当t=时取得最小值,最小值为2+3,即k≤2+3. ∴k的取值范围为(-∞,2+3]
10、【解答】(1)由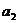 +
+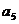 =12,
=12,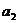
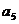 =27,且
=27,且 >0,所以
>0,所以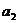 =3,
=3,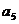 =9,
=9,
从而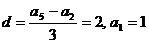 ,
,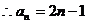
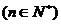
在已知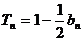 中,令n=1,得
中,令n=1,得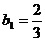
当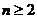 时,
时,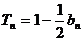 ,
,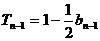 ,两式相减得,
,两式相减得,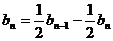 ,
,
(2)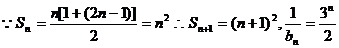
当n=1时,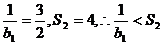 ,当n=2时,
,当n=2时,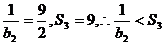 ,
,
当n=3时,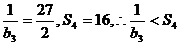 ,当n=4时,
,当n=4时,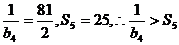 ,
,
猜想: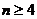 时,
时,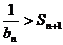 以下用数学归纳法证明:(i)n=4时,已证,
以下用数学归纳法证明:(i)n=4时,已证,
(ii)设n=k( 时,
时,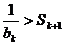 ,即
,即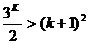 ,则n=k+1时,
,则n=k+1时,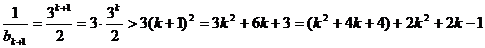
当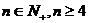 时,
时,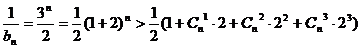
=
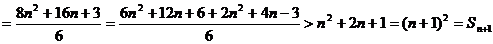 ,
,
综上所述,当n=1,2,3时,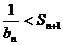 ,当
,当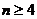 时,
时,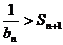
 www.1010jiajiao.com
www.1010jiajiao.com
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com