1．若的　　　　　　　　　　　　　　　　　 ( 　 )

　　　 A．充分不必要条件　　　　　　　　　　　　　　　　 B．必要不充分条件

　　　 C．充分必要条件　　　　　　　　　　　　　　　　　　 D．既不充分也不必要条件

21、已知两点和分别在直线和上运动，且，动点满足：为坐标原点)，点的轨迹记为曲线

　 (1)求曲线的方程，并讨论曲线的类型；

　 (2)过点(0，1)作直线与曲线。交于不同的两点、，若对于任意，都有为锐角，求直线的斜率的取值范围。

答案：(1)甲得是的中点

设依题意得:

消去，整理得

当时，方程表示焦点在轴上的椭圆；

当时，方程表示焦点在轴上的椭圆；

当时，方程表示圆。

(Ⅱ)由，焦点在轴上的椭圆，直线与曲线恒有两交点，

因为直线斜率不存在时不符合题意，

可设直线的方程为 ，直线与椭圆的交点为

_，

要使为锐角，则有

即_，可得，对于任意恒成立

而。

所以满足条件的的取值范围是

20. 已知抛物线 y ² = – x与直线 y = k ( x + 1 )相交于A、B两点, 点O是

坐标原点.

　 (1)求证: OA^OB;　

　 (2)当△OAB的面积等于时, 求k的值.

19、已知某食品厂需要定期购买食品配料，该厂每天需要食品配料200千克，配料的价格为元/千克，每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用，其标准如下: 7天以内(含7天)，无论重量多少，均按10元/天支付；超出7天以外的天数，根据实际剩余配料的重量，以每天0.03元/千克支付.

(Ⅰ)当9天购买一次配料时，求该厂用于配料的保管费用P是多少元？

(Ⅱ)设该厂天购买一次配料，求该厂在这天中用于配料的总费用(元)关于的函数关系式，并求该厂多少天购买一次配料才能使平均每天支付的费用最少?

答案：(Ⅰ)当9天购买一次时，该厂用于配料的保管费用

P=70+=88(元)　　　　　　　

　 (Ⅱ)(1)当x≤7时

y=360x+10x+236=370x+236　　　　　　　　　　　　　

　　　　 (2)当 x>7时

y=360x+236+70+6[()+()+……+2+1]　

　　　　　　　 =　　　　　　　　　　　　　　　

　　　　 ∴　　　　　　　　　　　　

　　　　 ∴设该厂x天购买一次配料平均每天支付的费用为f(x)元

当x≤7时

　 当且仅当x=7时　　　　　　　

f(x)有最小值(元)

当x＞7时

=≥393　　　　　　

　　 当且仅当x=12时取等号

∵393<404

∴当x=12时 f(x)有最小值393元　　　　　　　　　

答：(Ⅰ)当9天购买一次时，该厂用于配料的保管费用P为88元；

18、已知过点A(0，1)，且方向向量为，相交于点M、N.

(1)求实数的取值范围；　

(2)若O为坐标原点，且.

答案：(1)

由

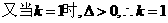
17、已知集合

　 (1)当=3时，求；

　 (2)若，求实数的值.

答案：由

，

(1)当m=3时，，

则

(2)

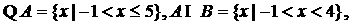
，此时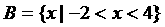，符合题意，故实数m的值为8.

16、已知直线，经过点的直线到的角等于45°，求直线的一般方程．

答案：直线：和

15、把椭圆=1的长轴AB五等份，过每个分点作AB的垂线，分别与椭圆的上半部分交于C、D、E、G四点，设F是椭圆的左焦点，则的值是　　　　 ．

答案：20

14、函数()的最小值为　　　　 ．

答案：25

13、已知关于的不等式＜0的解集，则实数　　　　 ．

答案：－2