
题目列表(包括答案和解析)
21、(本小题10分)
 如图,在平行四边形
如图,在平行四边形 中,
中, ,将它们沿对角线
,将它们沿对角线 折起,折后的点
折起,折后的点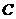 变为
变为 ,且
,且 .
.
(1)求点 到平面
到平面 的距离;
的距离;
(2) 为线段
为线段 上的一个动点,当线段
上的一个动点,当线段 的
的
长为多少时, 与平面
与平面 所成的角为
所成的角为 ?
?
20、设过点 的直线分别与
的直线分别与 轴的正半轴和
轴的正半轴和 轴的正半轴交于
轴的正半轴交于 、
、 两点,点
两点,点 与点
与点 关于
关于 轴对称,
轴对称, 为坐标原点,若
为坐标原点,若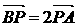 ,且
,且 ,则
,则 点的轨迹方程是(***)
点的轨迹方程是(***)
A.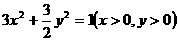 B.
B.
C. D.
D.
19、已知双曲线的两个焦点 ,过
,过 作垂直于实轴的直线交双曲线于
作垂直于实轴的直线交双曲线于 两点,若∠
两点,若∠ ,则双曲线的离心率
,则双曲线的离心率 等于(***)
等于(***)
A. B.
B. C.
C. D.
D.
18、已知 ,经计算得
,经计算得
 ,据此规律猜想,有*****;
,据此规律猜想,有*****;
17、 如图,甲站在水库底面上的点
如图,甲站在水库底面上的点 处,乙站在水
处,乙站在水
坝斜面上的点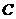 处,已知库底与水坝所成的二面角
处,已知库底与水坝所成的二面角
为 ,测得从
,测得从 到库底与水坝的交线的距离
到库底与水坝的交线的距离
分别为 米、
米、 米,
米, 米,
米,
则甲乙两人相距*****米.
16、(本小题12分)
已知抛物线 与直线
与直线 相交于
相交于 两点,
两点, .
.
(1)
求 的值;
的值;
(2)设P 是x轴上的一点,当△ 的面积为39时,求点P的坐标.
的面积为39时,求点P的坐标.
第II卷 共50分
15、(本小题13分)
 如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
(1)证明:PA//平面BDE;
(2)求二面角B-DE-C大小的余弦值;
(3)在棱PB上是否存在点F,使PB⊥平面DEF?证明你的结论.
14、(本小题10分)
设命题 关于
关于 的方程
的方程 无实根, 命题
无实根, 命题 关于
关于 的不等式
的不等式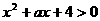 的解集为
的解集为 . 如果命题“
. 如果命题“

 ”为假命题,“
”为假命题,“
 ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围.
13、以下四个命题中:① “若x2+y2≠0,则x,y全不为零”的否命题;
②若 、
、 、
、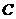 三点不共线,对平面
三点不共线,对平面 外的任一点
外的任一点 ,有
,有 ,则点
,则点 与点
与点 、
、 、
、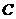 共面;
共面;
③若双曲线 的两焦点为
的两焦点为 ,点
,点 为双曲线上一点,且
为双曲线上一点,且 ,则
,则 的面积为16;
的面积为16;
④曲线 与曲线
与曲线 (0﹤k﹤9)有相同的焦点;
(0﹤k﹤9)有相同的焦点;
其中真命题的序号为*****.
12、若双曲线 的焦距为
的焦距为 ,则
,则 的值为*****;
的值为*****;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com