
题目列表(包括答案和解析)
3.“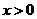 ”是“
”是“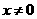 ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
2.一个等比数列前n项和为48,前2n项和为60,则前3n项和为( )
A.83 B.108 C.75 D.63
1.已知数列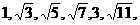 …
…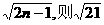 是这个数列的第( )项
是这个数列的第( )项
A.10 B.11 C.12 D.21
22. 解:(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以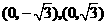 为焦点,长半轴为2的椭圆.它的短半轴
为焦点,长半轴为2的椭圆.它的短半轴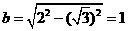 ,故曲线C的方程为
,故曲线C的方程为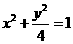 .
.
设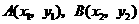 ,其坐标满足
,其坐标满足
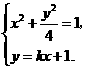 消去y并整理得
消去y并整理得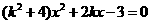 ,
,
故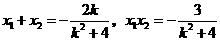 .
.
若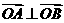 ,即
,即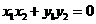 .而
.而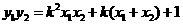 ,k+s-5#u
,k+s-5#u 
于是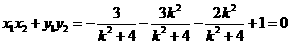 ,
,
化简得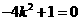 ,所以
,所以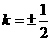 .
.
(Ⅱ)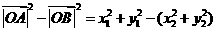
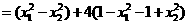
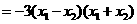
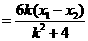 .
.
因为A在第一象限,故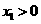 .由
.由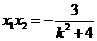 知
知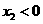 ,从而
,从而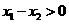 .又
.又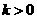 ,
,
故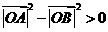 ,
,
即在题设条件下,恒有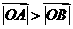 .
.
21.解:(I)矩形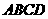 中,
中,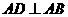 ,
,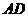 边所在直线的斜率为
边所在直线的斜率为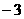 ,且过点
,且过点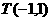 ,则
,则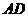 边所在直线的方程为:
边所在直线的方程为: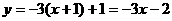 ;即
;即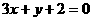
(II)矩形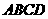 外接圆圆心为对角线交点
外接圆圆心为对角线交点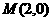 ,又
,又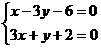 解得
解得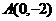 ,
,
所以外接圆半径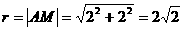 ,外接圆的方程为:
,外接圆的方程为: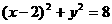 k+s-5#u
k+s-5#u 
(III)设动圆 的圆心坐标为
的圆心坐标为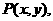 由题意可知:
由题意可知:
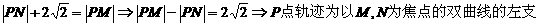 ,它的轨迹方程为:
,它的轨迹方程为: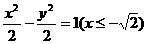
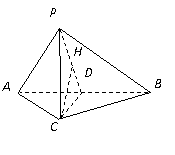
20.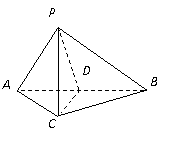 解法一:
解法一:
(Ⅰ)取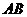 中点
中点 ,连结
,连结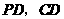 .
.
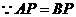 ,
,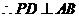 .
.
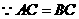 ,
,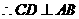 .
.
 ,
,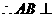 平面
平面 .
.
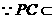 平面
平面 ,
,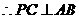 .
.
(Ⅱ)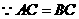 ,
,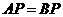 ,
,
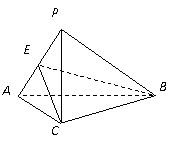
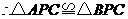 .
.
又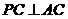 ,
,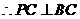 .
.
又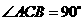 ,即
,即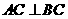 ,且
,且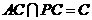 ,
,
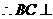 平面
平面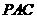 .
.
取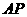 中点
中点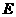 .连结
.连结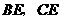 .
.
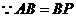 ,
,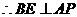 .
.
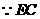 是
是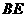 在平面
在平面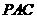 内的射影,
内的射影,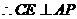 .
.
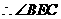 是二面角
是二面角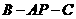 的平面角.
的平面角.
在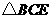 中,
中,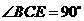 ,
,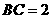 ,
,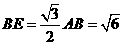 ,
,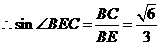 .k+s-5#u
.k+s-5#u 
 二面角
二面角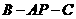 的大小为
的大小为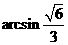 .
.
(Ⅲ)由(Ⅰ)知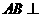 平面
平面 ,
,
 平面
平面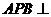 平面
平面 .
.
过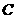 作
作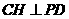 ,垂足为
,垂足为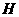 .
.
 平面
平面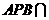 平面
平面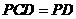 ,
,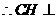 平面
平面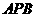 .
.
 的长即为点
的长即为点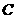 到平面
到平面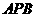 的距离.
的距离.
由(Ⅰ)知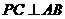 ,又
,又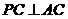 ,且
,且 ,
,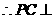 平面
平面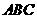 .
.
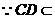 平面
平面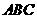 ,
,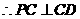 .
.
在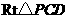 中,
中,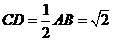 ,
,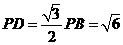 ,
,
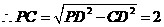 .
.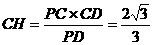 .
.
 点
点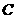 到平面
到平面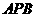 的距离为
的距离为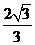 .
.
解法二:(Ⅰ)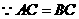 ,
,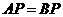 ,
,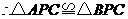 .k+s-5#u
.k+s-5#u 
又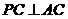 ,
,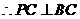 .
.
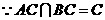 ,
,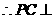 平面
平面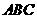 .
.
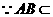 平面
平面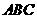 ,
,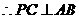 .
.
(Ⅱ)如图,以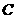 为原点建立空间直角坐标系
为原点建立空间直角坐标系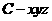 .
.
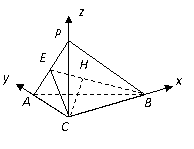 则
则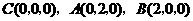 .设
.设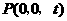 .
.
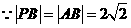 ,
,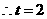 ,
,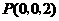 .
.
取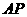 中点
中点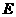 ,连结
,连结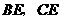 .
.
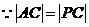 ,
,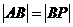 ,
,
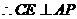 ,
,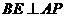 .
.
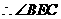 是二面角
是二面角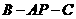 的平面角.
的平面角.
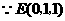 ,
,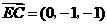 ,
,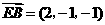 ,
,
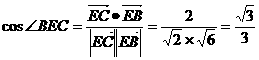 .k+s-5#u
.k+s-5#u 
 二面角
二面角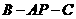 的大小为
的大小为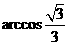 .
.
(Ⅲ)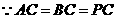 ,
,
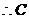 在平面
在平面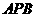 内的射影为正
内的射影为正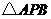 的中心
的中心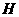 ,且
,且 的长为点
的长为点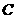 到平面
到平面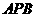 的距离.
的距离.
如(Ⅱ)建立空间直角坐标系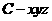 .
.
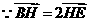 ,
, 点
点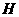 的坐标为
的坐标为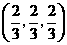 .
.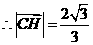 .
.
 点
点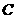 到平面
到平面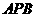 的距离为
的距离为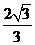 .k+s-5#u
.k+s-5#u 
19. (I)记“恰有2条线路没有被选”为事件A,则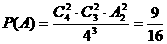
(II)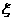 可能取值为0,1,2,3 则
可能取值为0,1,2,3 则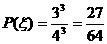 ;
;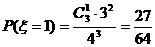
 ,
,
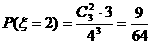 ,
,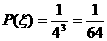 ∴的分布列为
∴的分布列为
|
|
0 |
1 |
2 |
3 |
|
P |
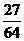 |
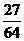 |
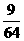 |
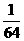 |
∴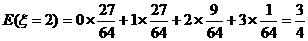
18.解:(Ⅰ)解法一:设“甲投球一次命中”为事件A,“乙投球一次命中”为事件B.
则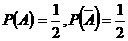 .
.
故甲投球2次至少命中1次的概率为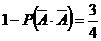
解法二:由题设和(Ⅰ)知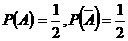 k+s-5#u
k+s-5#u 
故甲投球2次至少命中1次的概率为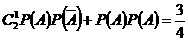
(Ⅱ)由题意得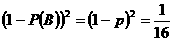 解得
解得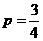 或
或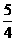 (舍去),
(舍去),
所以乙投球的命中率为 .
. 所以
所以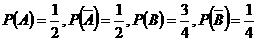
甲、乙两人各投球2次,共命中2次有三种情况:甲、乙两人各中一次;甲中两次,乙两次均不中;甲两次均不中,乙中2次。概率分别为
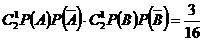 ,
,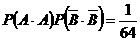 ,
,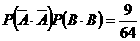
所以甲、乙两人各投两次,共命中2次的概率为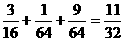
17.解: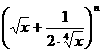 的展开式中前三项的系数分别为
的展开式中前三项的系数分别为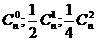 ,由题意知
,由题意知
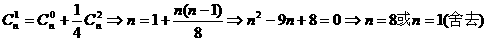
(Ⅰ)设展开式中含有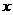 的项为
的项为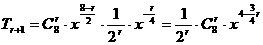 ;k+s-5#u
;k+s-5#u 
则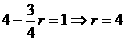 ,含有
,含有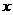 的项为第5项,它的系数为
的项为第5项,它的系数为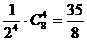
(Ⅱ)设展开式中第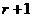 项为有理项,则
项为有理项,则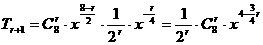
当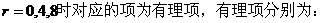
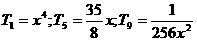
13.2
14.10 15.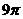 16.96
16.96
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com