
题目列表(包括答案和解析)
6.若实数x,y满足 则z = 2x + 3y的最小值为
则z = 2x + 3y的最小值为
A.3 B.4 C.5 D.不存在
5.若双曲线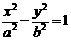 (a,b>0)的渐近线与圆x2 +(y-3)2 = 3相切,则双曲线的离心率为
(a,b>0)的渐近线与圆x2 +(y-3)2 = 3相切,则双曲线的离心率为
A.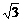 B.
B.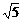 C.2
D.3w.w.^w.k.s.5*
C.2
D.3w.w.^w.k.s.5*
4.两条直线x +(1 + m)y + m-2 = 0与mx + 2y + 8 = 0平行的充要条件是
A.m = 1或-2 B.m = 1 C.m =-2
D.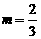
3.不等式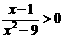 的解集为w.w.^w.k.s.5*
的解集为w.w.^w.k.s.5*
A.(-3,1) B.(3,+∞)
C.(-∞,-3)∪(1,+∞) D.(-3,1)∪(3,+∞)
2.若a<b<0,则下列不等关系中,不成立的是
A.︱a︱>︱b︱ B.a2>b2 C.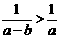 D.
D.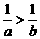
1.直线x = 1的倾斜角为
A.0
B.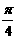 C.
C. D.不存在
D.不存在
20.(本小题满分14分)已知椭圆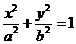
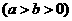 的右焦点
的右焦点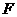 在抛物线
在抛物线 的准线上.
的准线上.
(1)若椭圆的离心率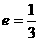 ,求椭圆的方程;
,求椭圆的方程;
 (2)设过点
(2)设过点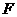 的直线
的直线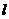 交椭圆于
交椭圆于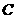 、
、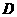 两点,若直线
两点,若直线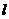 绕点
绕点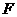 任意转动时恒有
任意转动时恒有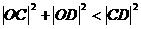 ,其中
,其中 为坐标原点,求
为坐标原点,求 的取值范围.
的取值范围.
19. (本小题满分14分)已知数列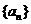 的前
的前 项和为
项和为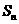 ,其中
,其中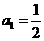 ,
,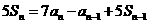
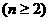 ;等差数列
;等差数列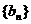 ,其中
,其中 ,
,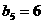 .
.
(1)求数列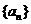 的通项公式;
的通项公式;
(2)若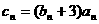 ,求数列
,求数列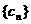 的前
的前 项和
项和 ;
;
(3)若自然数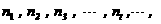 (
( 为正整数)满足
为正整数)满足 <
< 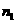 <
< <
<  <
< 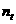 <
< ,使得
,使得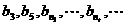 成等比数列,请用
成等比数列,请用 表示
表示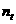 .
.
18. (本小题满分14分)如图,正三棱柱
(本小题满分14分)如图,正三棱柱 中,
中,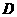 是
是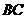 的
的
中点,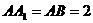 .
.
(1)求证: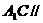 平面
平面 ;
;
(2)求二面角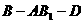 的平面角的正切值;
的平面角的正切值;
(3)在棱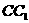 上是否存在一点
上是否存在一点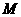 ,使得三棱锥
,使得三棱锥 的体积
的体积
为 ?若存在,请确定点
?若存在,请确定点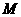 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
17. (本小题满分14分)某工厂生产甲、乙两种产品,已知生产每吨甲种产品所需煤9吨、电力4千瓦时、劳力3个,获得利润6万元;生产每吨乙种产品所需煤4吨、电力5千瓦时、劳力10个,获得利润12万元;每天资源限额(最大供应量)分别为煤360吨、电力200千瓦时、劳动力300个.问:每天生产甲、乙两种产品各多少吨,获得利润总额最大?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com