
题目列表(包括答案和解析)
7. 如图,已知点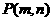
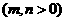 为椭圆
为椭圆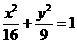 上,以点
上,以点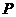 为一个顶点的内接矩形
为一个顶点的内接矩形 的面积最大值为
的面积最大值为
A.24 B.18 C.12 D.6
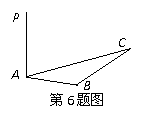
6. 如图,已知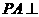 平面
平面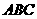 ,
,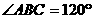 ,
,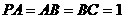 ,则
,则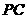 等于
等于
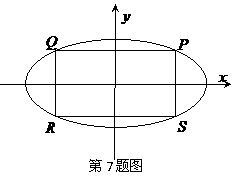 A.1 B.
A.1 B.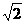 C.
C.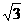 D.2
D.2
5. 已知双曲线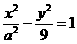
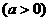 的一条渐近线方程为
的一条渐近线方程为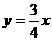 ,则该双曲线的离心率等于
,则该双曲线的离心率等于
 A.
A. 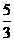 B.
B. 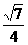 C.
C. 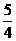 D.
D. 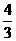
4. 不等式组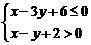 表示的平面区域是( )
表示的平面区域是( )
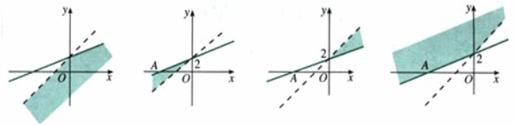
A. B. C. D.
3. 设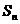 是等差数列
是等差数列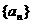 的前
的前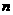 项和,若
项和,若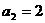 ,
,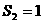 ,则公差
,则公差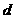 等于
等于
A.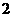 B.
B.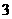 C.
C.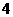 D.
D.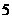
2. 在△ABC中,已知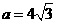 ,
,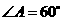 ,
,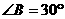 ,则边长
,则边长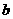 等于
等于
A.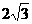 B.
B.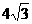 C.4 D. 12
C.4 D. 12
1.命题“若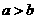 ,则
,则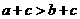 ”的逆命题为
”的逆命题为
A.若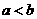 ,则
,则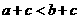 B.若
B.若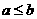 ,则
,则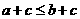
C.若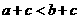 ,则
,则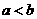 D.若
D.若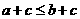 ,则
,则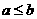
20.(本小题满分14分)已知数列{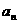 }中,
}中,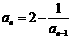 (n≥2,
(n≥2,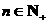 ),
),
(1)若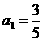 ,数列
,数列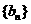 满足
满足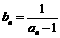 (
(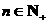 ),求证数列{
),求证数列{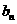 }是等差数列;
}是等差数列;
(2)若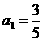 ,求数列{
,求数列{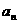 }中的最大项与最小项,并说明理由;
}中的最大项与最小项,并说明理由;
(3)若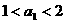 ,试证明:
,试证明: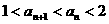 .
.







19.(本小题满分14分一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数:f1(x)=x,f2(x)=x2,f3(x)=x3,f4(x)=sinx,f5(x)=cosx,f6(x)=2.
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数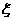 的分布列和数学期望.
的分布列和数学期望.
18.(本小题满分14分) 有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
|
|
优秀 |
非优秀 |
总计 |
|
甲班 |
10 |
|
|
|
乙班 |
|
30 |
|
|
合计 |
|
|
105 |
已知在全部105人中抽到随机抽取1人为优秀的概率为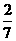
(Ⅰ)请完成上面的列联表;
(Ⅱ)根据列联表的数据,若按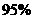 的可靠性要求,能否认为“成绩与班级有关系” .
的可靠性要求,能否认为“成绩与班级有关系” .
(Ⅲ)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到6或10号的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com