
题目列表(包括答案和解析)
12.(1)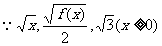 成等差数列,∴
成等差数列,∴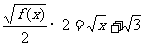
∴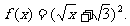
∵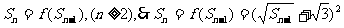 ,
,
∴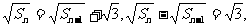
∴{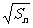 }是以
}是以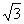 为公差的等差数列.
为公差的等差数列.
∵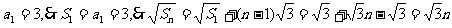 ,
,
∴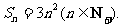
∴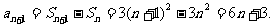
(2)∵数列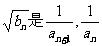 的等比中项,∴
的等比中项,∴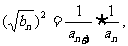
∴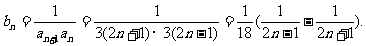
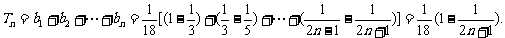 ……
……
11.解析:
(1)曲线方程为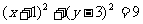 ,表示圆心为(-1,3),半径为3的圆.
,表示圆心为(-1,3),半径为3的圆.

∴圆心(-1,3)在直线上,代入直线方程得m=-1.
(2)∵直线PQ与直线y=x+4垂直,
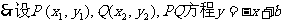
将直线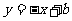 代入圆方程. 得
代入圆方程. 得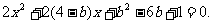
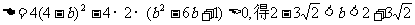
由韦达定理得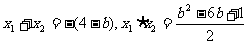
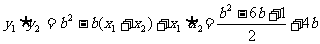

10.(1)平行四边形
(2)略
9.解:(1)由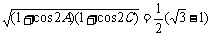 得
得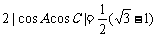
即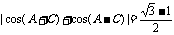 而
而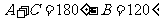 及△ABC为锐角三角形
及△ABC为锐角三角形
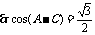 又
又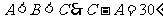 且C+A=120°∴C=75°,B=60°,A=45°
且C+A=120°∴C=75°,B=60°,A=45°
(2)由(1)及正弦定理得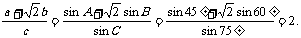
7、(1)a=0.45,m=6 (2)略
8解 (1)
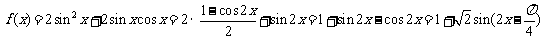
∴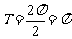
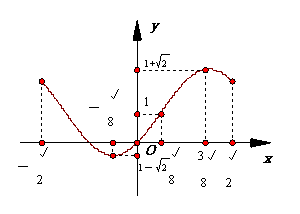 如图最大值为
如图最大值为 ,最小值为
,最小值为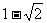
6.(1)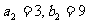
(2)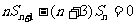 ,即
,即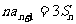 ①
①
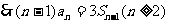 ②
②
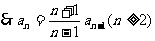
①-②得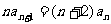 ,
,
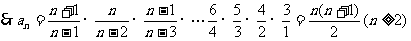
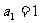 也适合上式
也适合上式
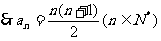
由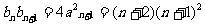 得
得
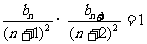 ,令
,令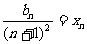 ,即
,即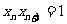
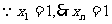 ,
,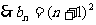
5.(1)由已知得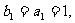 且
且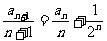 ,
,
即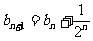 ,
,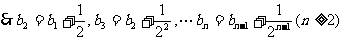 ,
,
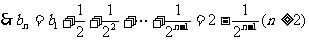 ,
,
又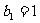 ,
,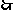 所求数列
所求数列 的通项公式为
的通项公式为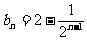 ;
;
(2)由(1)知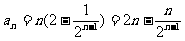 ,
,
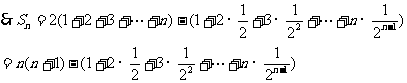
令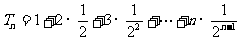
 ①
①
则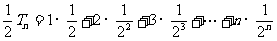 ②
②
①-②得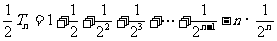 ,
,
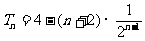 ,
,
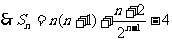
(文科)(1)由已知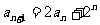 得
得
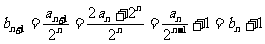 ,
,
又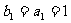
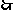
 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;
(2)由(1)知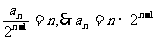
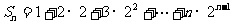
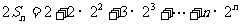
两式相减得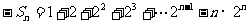
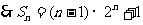
4.解:连接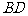 ,则四边形
,则四边形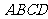 的面积
的面积
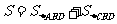 =
=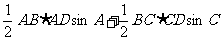
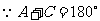 ,
,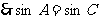
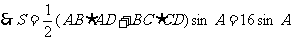
由余弦定理
在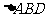 中,
中,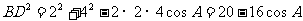
在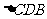 中,
中,
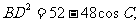
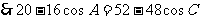 ,
,
又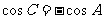 ,
, 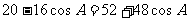 ,
,
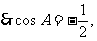
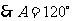
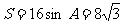
3.解:由已知得:
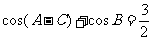 ,
, 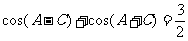 ,
,
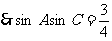 ,
,
又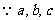 成等比数列,
成等比数列, 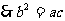 ,
,
又由正弦定理得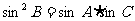 ,
,
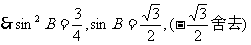 ,
,
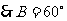 或
或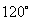 ,
,
但若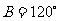 则
则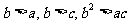 这与已知
这与已知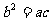 矛盾,
矛盾,
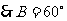
2.解:设等差数列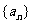 项数为
项数为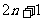 ,
,
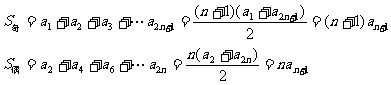
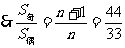 ,解得
,解得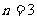 ,
,
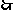 项数
项数 ,
,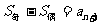 ,
,
即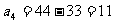 为所求中间项。
为所求中间项。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com