
题目列表(包括答案和解析)
6.四面体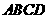 的外接球球心在
的外接球球心在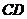 上,且
上,且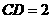 ,
,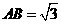 ,则在外接球球面上
,则在外接球球面上 ,
,
 两点间的球面距离是( )
两点间的球面距离是( )
A.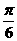 B.
B.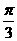 C.
C.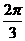 D.
D.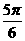
5.在空间中,有如下命题:
①互相平行的两条直线在同一个平面内的射影必然是互相平行的两条直线;
②若平面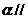 平面
平面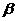 ,则平面
,则平面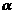 内任意一条直线
内任意一条直线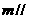 平面
平面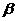 ;
;
③若平面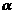 与平面
与平面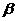 的交线为
的交线为 ,平面
,平面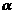 内的直线
内的直线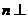 直线
直线 ,则直线
,则直线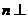 平面
平面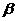 ;
;
④若平面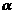 内的三点A,B,C到平面
内的三点A,B,C到平面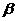 的距离相等,则
的距离相等,则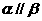 。
。
其中正确命题的个数为( )个
A.0 B.1 C.2 D.3
4.已知钝角三角形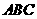 的最大边长为2,其余两边长为
的最大边长为2,其余两边长为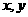 ,则以
,则以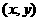 为坐标的点所
为坐标的点所
表示平面区域的面积是( )
A.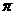 B.
B.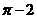 C.
C.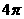 D.
D.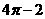
3.与直线l1: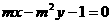 垂直于点P(2,1)的直线l2的方程为( )
垂直于点P(2,1)的直线l2的方程为( )
A.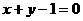 B.
B.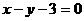
C.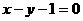 D.
D.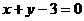
2.抛物线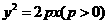 的准线经过等轴双曲线
的准线经过等轴双曲线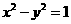 的左焦点,则
的左焦点,则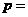 ( )
( )
A.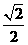 B.
B.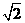 C.
C.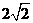 D.
D.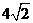
1.直线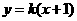 与圆
与圆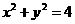 的位置关系是( )
的位置关系是( )
A.相交 B.相切 C.相离 D.与k的取值有关
21.(本小题满分13分)
已知函数f (x)=a[lnx−ln(1−x)]−2x( 0<x<1 ).
(Ⅰ)若函数f (x)是单调函数, 求实数a的取值范围;
(Ⅱ)求f (x)=0在区间(0 ,1)内的根的个数.
20.(本小题满分13分)
已知椭圆C的长轴的两个端点分别为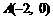 ,
,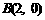 ,过右焦点F且垂直于长轴的弦长为3,
点P是椭圆C上异于A, B的一动点,直线AP,BP与直线l:x=a (FÏl)分别相交于M, N两点,记直线FM,FN的斜率的乘积为u .
,过右焦点F且垂直于长轴的弦长为3,
点P是椭圆C上异于A, B的一动点,直线AP,BP与直线l:x=a (FÏl)分别相交于M, N两点,记直线FM,FN的斜率的乘积为u .
(Ⅰ)求椭圆C的方程;
(Ⅱ)对于给定的常数a,证明u是一个与P的位置无关的常数;
(Ⅲ)当a变化时, 求u的最小值.
19.(本小题满分13分)
某人在同一城市开了两家小店,每家店各有 名员工.节日期间,每名员工请假的概率都是
名员工.节日期间,每名员工请假的概率都是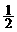 ,且是否请假互不影响.若某店的员工全部请假,而另一家店没有人请假,则调剂
,且是否请假互不影响.若某店的员工全部请假,而另一家店没有人请假,则调剂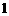 人到该店以维持正常运转,否则该店就关门停业.计算:
人到该店以维持正常运转,否则该店就关门停业.计算:
(Ⅰ)有人被调剂的概率;
(Ⅱ)停业的店铺数X的分布列和数学期望.
18.(本小题满分12分)
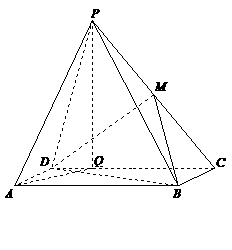 如图,四棱锥
如图,四棱锥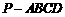 中,底面
中,底面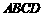 是矩形,
是矩形,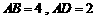 ,点
,点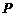 在底面的射影
在底面的射影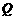 在
在 上,且
上,且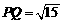 ,
,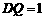 .
.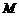 为
为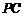 的中点.
的中点.
(Ⅰ)证明 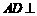 平面
平面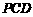 ;
;
(Ⅱ)求直线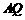 与平面
与平面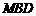 所成的角.
所成的角.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com