4．重复几次，得到3-5条打好点的纸带。

3．接通电源，松开纸带，让重锤自由下落。

2．把纸带的一端在重锤上用夹子固定好，另一端穿过计时器限位孔，竖直提起纸带使重锤停靠在打点计时器附近，纸带上端用夹子夹住。

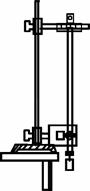
1．按如图装置把打点计时器安装在铁架台上，用导线把打点计时器与学生电源连接好。

　 　铁架台(带铁夹)，打点计时器，学生电源，导线，带铁夹的重缍，纸带，米尺。

当物体自由下落时，只有重力做功，物体的重力势能和动能互相转化，机械能守恒。若某一时刻物体下落的瞬时速度为v，下落高度为h，则应有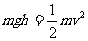：，借助打点计时器，测出重物某时刻的下落高度h和该时刻的瞬时速度v，即可验证机械能是否守恒， 实验装置如图所示。测定第n点的瞬时速度的方法是：测出第n点的相邻前、后两段相等时间T内下落的距离s_n和s_n+1，由公式 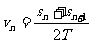，或由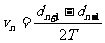算出,如图所示。

验证机械能守恒定律

17．宇宙中存在一些离其它恒星较远的、由质量相等的三颗星组成的三星系统，通常可忽略其它星体对它们的引力作用。已观测到稳定的三星系统存在两种基本的构成形式：一种是三颗星位于同一直线上，两颗星围绕中央星在同一半径为R的圆轨道上运行；另一种形式是三颗星位于等边三角形的三个项点上，并沿外接于等边三角形的圆形轨道运行。设每个星体的质量均为。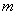

(1)试求第一种形式下，星体运动的线速度和周期。

(2)假设两种形式星体的运动周期相同，第二种形式下星体之间的距离应为多少？

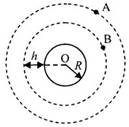
16．如图所示，A是地球的同步卫星．另一卫星B的圆形轨道位于赤道平面内，离地面高度为h．已知地球半径为R，地球自转角速度为ω₀，地球表面的重力加速度为g，O为地球中心．

　　 (1)求卫星B的运行周期．

　　 (2)如卫星B绕行方向与地球自转方向相同，某时刻A、B两卫星相距最近(O、B、A在同一直线上)，则至少经过多长时间，他们再一次相距最近?

答案 　 T_B=2π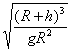　　　　　　 t=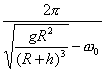

15.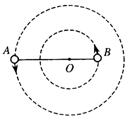神奇的黑洞是近代引力理论所预言的一种特殊天体，探寻黑洞的方案之一是观测双星系统的运动规律。天文学家观测河外星系大麦哲伦云时，发现了LMCX-3双星系统，它由可见星A和不可见的暗星B构成。两星视为质点，不考虑其它天体的影响，A、B围绕两者连线上的O点做匀速圆周运动，它们之间的距离保持不变，如图所示。引力常量为G，由观测能够得到可见星A的速率v和运行周期T。

(1)可见星A所受暗星B的引力F_A可等效为位于O点处质量为m′的星体(视为质点)对它的引力，设A和B的质量分别为m₁、m₂，试求m′(用m₁、m₂表示)；

(2)求暗星B的质量m₂与可见星A的速率v、运行周期T和质量m₁之间的关系式；

(3)恒星演化到末期，如果其质量大于太阳质量m_s的2倍，它将有可能成为黑洞。若可见星A的速率v=2.7×10⁵m/s，运行周期T=4.7π×10⁴s，质量m₁=6m_s，试通过估算来判断暗星B有可能是黑洞吗?(G=6.67×10^-11N·m²/kg²，m_s=2.0×10³⁰kg)

答案 (1)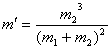(2)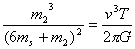(3)暗星B有可能是黑洞。