
题目列表(包括答案和解析)
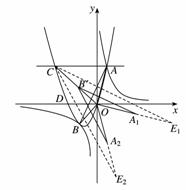
9、如图,抛物线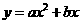 (a
(a 0)与反比例函数
0)与反比例函数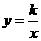 的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点).
的图像相交于点A,B. 已知点A的坐标为(1,4),点B(t,q)在第三象限内,且△AOB的面积为3(O为坐标原点).
(1)求反比例函数的解析式
(2)用含t的代数式表示直线AB的解析式;
(3)求抛物线的解析式;
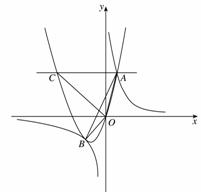
 (4)过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,把△AOB绕点O逆时针旋转90º,请在图②中画出旋转后的三角形,并直接写出所有满足△EOC∽△AOB的点E的坐标.
(4)过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,把△AOB绕点O逆时针旋转90º,请在图②中画出旋转后的三角形,并直接写出所有满足△EOC∽△AOB的点E的坐标.
解:(1)因为点A(1,4)在双曲线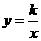 上,
上,
所以k=4. 故双曲线的函数表达式为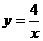 . ……………………………………… 1分
. ……………………………………… 1分
(2)设点B(t,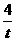 ),
),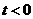 ,AB所在直线的函数表达式为
,AB所在直线的函数表达式为 ,则有
,则有
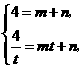 解得
解得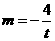 ,
,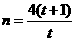 .
.
直线AB的解析式为y= - x+ ………………………………………… 3分
 (3)直线AB与y轴的交点坐标为
(3)直线AB与y轴的交点坐标为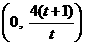 ,故
,故
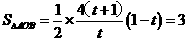 ,整理得
,整理得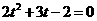 ,
,
解得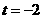 ,或t=
,或t=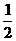 (舍去).所以点B的坐标为(
(舍去).所以点B的坐标为(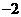 ,
,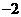 ).
).
因为点A,B都在抛物线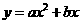 (a
(a 0)上,所以
0)上,所以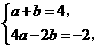 解得
解得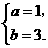
所以抛物线的解析式为y=x2+3x ……………… 4分
(4)画出图形………………………………………………2分
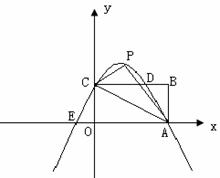 点
点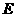 的坐标是(8,
的坐标是(8,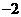 ),或(2,
),或(2,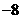 )……………… 2分
)……………… 2分
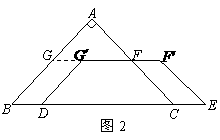
8、如图1,在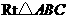 中,
中,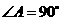 ,
,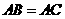 ,
,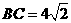 ,另有一等腰梯形
,另有一等腰梯形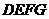 (
(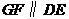 )的底边
)的底边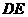 与
与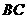 重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
(1)直接写出△AGF与△ABC的面积的比值;
(2)操作:固定 ,将等腰梯形
,将等腰梯形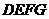 以每秒1个单位的速度沿
以每秒1个单位的速度沿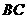 方向向右运动,直到点
方向向右运动,直到点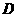 与点
与点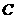 重合时停止.设运动时间为
重合时停止.设运动时间为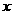 秒,运动后的等腰梯形为
秒,运动后的等腰梯形为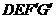 (如图2).
(如图2).
①探究1:在运动过程中,四边形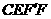 能否是菱形?若能,请求出此时
能否是菱形?若能,请求出此时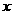 的值;若不能,请说明理由.
的值;若不能,请说明理由.
②探究2:设在运动过程中 与等腰梯形
与等腰梯形 重叠部分的面积为
重叠部分的面积为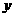 ,求
,求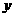 与
与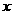 的函数关系式.
的函数关系式.
解:(1)△AGF与△ABC的面积比是1:4. (3分)
(2)①能为菱形. (1分)
由于FC∥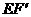 ,CE∥
,CE∥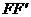 ,
,
 四边形
四边形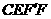 是平行四边形. (1分)
是平行四边形. (1分)
当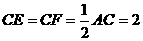 时,四边形
时,四边形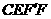 为菱形,( 1分)
为菱形,( 1分)
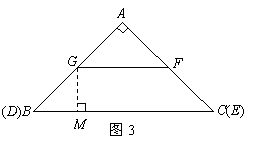 此时可求得
此时可求得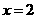 .
.
 当
当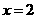 秒时,四边形
秒时,四边形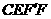 为 (1分)
为 (1分)
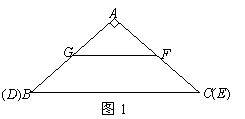
②分两种情况:
①当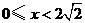 时,
时,
如图3过点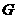 作
作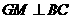 于
于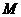 .
.
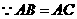 ,
,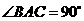 ,
,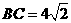 ,
, 为
为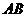 中点,
中点,
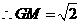 .
.
又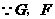 分别为
分别为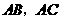 的中点,
的中点,
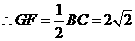 . ( 1分)
. ( 1分)
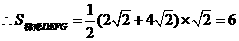
 等腰梯形
等腰梯形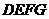 的面积为6.
的面积为6.
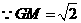 ,
,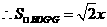 .
.
 重叠部分的面积为:
重叠部分的面积为: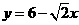 . ( 1分)
. ( 1分)
 当
当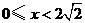 时,
时,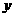 与
与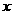 的函数关系式为
的函数关系式为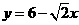 . ( 1分)
. ( 1分)
②当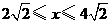 时,
时,
设 与
与 交于点
交于点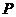 ,则
,则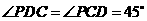 .
.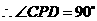 ,
,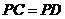 ,
,
作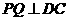 于
于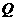 ,则.
,则. ( 1分)
( 1分)
 重叠部分的面积为:
重叠部分的面积为:
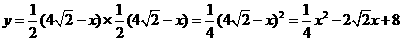 .
.
综上,当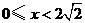 时,
时,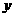 与
与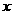 的函数关系式为
的函数关系式为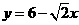 ;当
;当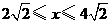 时,
时,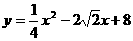 ( 1分)
( 1分)
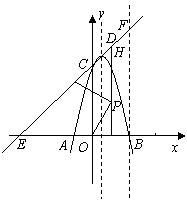
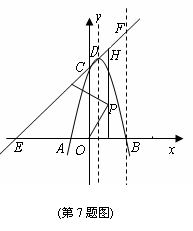
7、如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E,过点B作x轴的垂线,交直线CD于点F,在坐标平面内找一点G,使以点G、F、C为顶点的三角形与△COE相似,请直接写出符合要求的,并在第一象限的点G的坐标;
(3)在线段OB的垂直平分线上是否存在点P,使得点P到直线CD的距离等于点P到原点O的距离?如果存在,求出点P的坐标;如果不存在,请说明理由;
(4)将抛物线沿其对称轴平移,使抛物线与线段EF总有公共点.试探究:抛物线向上最多可平移多少个单位长度?
解:(1)设抛物线解析式为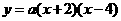 ,
,
把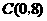 代入得
代入得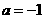 .……………1分
.……………1分
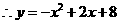
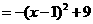 ,顶点
,顶点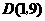 ……………2分
……………2分
(2)G(4,8), G(8,8), G(4,4) ……………3分
(3)假设满足条件的点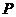 存在,依题意设
存在,依题意设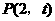 ,
,
由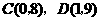 求得直线
求得直线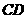 的解析式为
的解析式为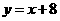 …………1分
…………1分
它与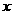 轴的夹角为
轴的夹角为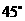 ,设
,设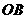 的中垂线交
的中垂线交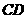 于
于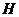 ,则
,则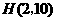 .
.
则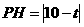 ,点
,点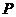 到
到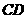 的距离为
的距离为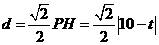 .
.
又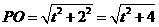 .
.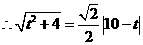 .
.
平方并整理得: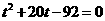 ,
,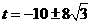 .……………1分
.……………1分
 存在满足条件的点
存在满足条件的点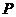 ,
,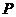 的坐标为
的坐标为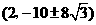 .……………1分
.……………1分
(4)由上求得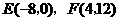 .
.
抛物线向上平移,可设解析式为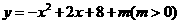 .
.
当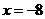 时,
时,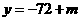 .
.
当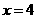 时,
时,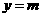 .
.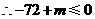 或
或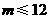 .……………1分
.……………1分
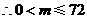 .
.
∴向上最多可平移72个单位长。……………2分
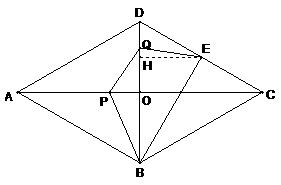
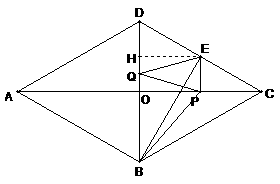
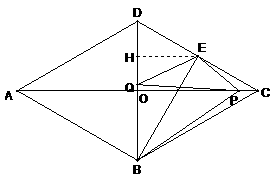
6、如图,在菱形ABCD中,AB=2cm,∠BAD=60°,E为CD边中点,点P从点A开始沿AC方向以每秒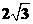 cm的速度运动,同时,点Q从点D出发沿DB方向以每秒1cm的速度运动,当点P到达点C时,P,Q同时停止运动,设运动的时间为x秒.
cm的速度运动,同时,点Q从点D出发沿DB方向以每秒1cm的速度运动,当点P到达点C时,P,Q同时停止运动,设运动的时间为x秒.
(1)当点P在线段AO上运动时.
①请用含x的代数式表示OP的长度;
②若记四边形PBEQ的面积为y,求y关于x的函数关系式(不要求写出自变量的取值范围);
 (2)显然,当x=0时,四边形PBEQ即梯形ABED,请问,当P在线段AC的其他位置时,以P,B,E,Q为顶点的四边形能否成为梯形?若能,求出所有满足条件的x的值;若不能,请说明理由.
(2)显然,当x=0时,四边形PBEQ即梯形ABED,请问,当P在线段AC的其他位置时,以P,B,E,Q为顶点的四边形能否成为梯形?若能,求出所有满足条件的x的值;若不能,请说明理由.
解:(1)①由题意得∠BAO=30°,AC⊥BD
∵AB=2 ∴OB=OD=1,OA=OC=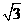
∴OP=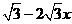 ……………2分
……………2分
②过点E作EH⊥BD,则EH为△COD的中位线
∴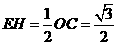 ∵DQ=x ∴BQ=2-x
∵DQ=x ∴BQ=2-x
∴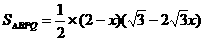 …………………………1分
…………………………1分
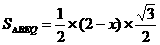 …………………………1分
…………………………1分
∴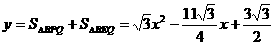 …………………………2分
…………………………2分
 (2)能成为梯形,分三种情况:
(2)能成为梯形,分三种情况:
当PQ∥BE时,∠PQO=∠DBE=30°
∴
即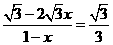 ∴x=
∴x=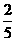
此时PB不平行QE,
∴x=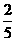 时,四边形PBEQ为梯形.
………………………2分
时,四边形PBEQ为梯形.
………………………2分
当PE∥BQ时,P为OC中点
 ∴AP=
∴AP=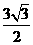 ,即
,即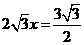
∴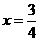
此时,BQ=2-x=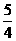 ≠PE,
≠PE,
 ∴x=
∴x=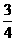 时,四边形PEQB为梯形.
…………………2分
时,四边形PEQB为梯形.
…………………2分
当EQ∥BP时,△QEH∽△BPO
∴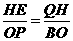 ∴
∴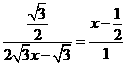
∴x=1(x=0舍去)
此时,BQ不平行于PE,
∴x=1时,四边形PEQB为梯形. ………………………………2分
 综上所述,当x=
综上所述,当x=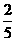 或
或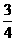 或1时,以P,B,E,Q为顶点的四边形是梯形.
或1时,以P,B,E,Q为顶点的四边形是梯形.
5、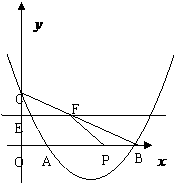 如图,抛物线
如图,抛物线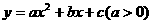 交
交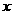 轴于A、B两点(A点在B点左侧),交
轴于A、B两点(A点在B点左侧),交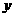 轴于点C,已知B(8,0),
轴于点C,已知B(8,0),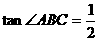 ,△ABC的面积为8.
,△ABC的面积为8.
(1)求抛物线的解析式;
(2)若动直线EF(EF∥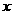 轴)从点C开始,以每秒1个长度单位的速度沿
轴)从点C开始,以每秒1个长度单位的速度沿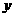 轴负方向平移,且交
轴负方向平移,且交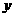 轴、线段BC于E、F两点,动点P同时从点B出发,在线段OB上以每秒2个单位的速度向原点O运动。连结FP,设运动时间
轴、线段BC于E、F两点,动点P同时从点B出发,在线段OB上以每秒2个单位的速度向原点O运动。连结FP,设运动时间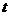 秒。当
秒。当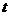 为何值时,
为何值时,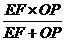 的值最大,并求出最大值;
的值最大,并求出最大值;
(3)在满足(2)的条件下,是否存在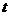 的值,使以P、B、F为顶点的三角形与△ABC相似。若存在,试求出
的值,使以P、B、F为顶点的三角形与△ABC相似。若存在,试求出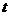 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
解:(1)由题意知 ∠COB = 90°B(8,0) OB=8 在Rt△OBC中tan∠ABC = 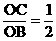
OC= OB×tan∠ABC = 8×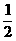 =4 ∴C(0,4)
=4 ∴C(0,4)
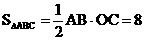 ∴AB = 4 A(4,0)
∴AB = 4 A(4,0)
把A、B、C三点的坐标带入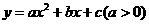 得
得 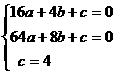 解得
解得 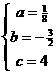
所以抛物线的解析式为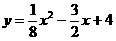 。
。
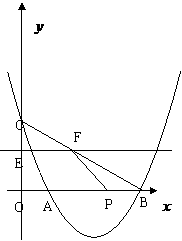 (2)C ( 0, 4 ) B ( 8, 0
) E ( 0, 4-t ) ( t > 0)
(2)C ( 0, 4 ) B ( 8, 0
) E ( 0, 4-t ) ( t > 0)
OC = 4 OB = 8 CE = t BP=2t OP =8-2t
∵EF // OB ∴△CEF -△COB
∴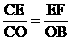 则有
则有 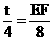 得 EF = 2t
得 EF = 2t
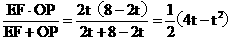 =
=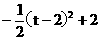
当t=2时 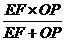 有最大值2.
有最大值2. 
(3)存在符合条件的t值,使△PBF与△ABC相似。
C ( 0, 4 ) B ( 8, 0 ) E ( 0, 4-t ) F(2t , 4 - t ) P ( 8-2t , 0 )
( t > 0)
AB = 4 BP=2t BF = 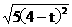
∵ OC = 4 OB = 8 ∴BC = 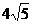
①当点P与A、F与C对应 则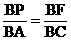 ,代入得
,代入得 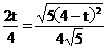 解得
解得 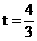

②当点P与C、F与A对应 则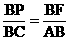 ,代入得
,代入得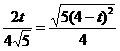 解得
解得 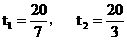 (不合题意,舍去)
(不合题意,舍去)
综上所述:符合条件的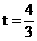 和
和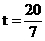 。
。
4、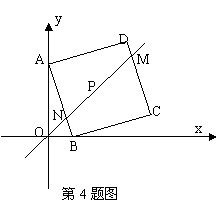 如图,P为正方形ABCD的对称中心,正方形ABCD的边长为
如图,P为正方形ABCD的对称中心,正方形ABCD的边长为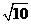 ,
,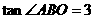 。直线OP交AB于N,DC于M,点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动,同时,点R从O出发沿OM方向以
。直线OP交AB于N,DC于M,点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动,同时,点R从O出发沿OM方向以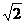 个单位每秒速度运动,运动时间为t。求:
个单位每秒速度运动,运动时间为t。求:
(1)分别写出A、C、D、P的坐标;
(2)当t为何值时,△ANO与△DMR相似?
(3)△HCR面积S与t的函数关系式;并求以A、B、C、R为顶点的
四边形是梯形时t的值及S的最大值。
解:解:(1) C(4,1)、D(3,4)、P(2,2)
…………………………………3分
(2)当∠MDR=450时,t=2,点H(2,0) ……………2分
当∠DRM=450时,t=3,点H(3,0) ……………2分
(3)S=-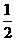 t2+2t(0<t≤4) ……… 1分
t2+2t(0<t≤4) ……… 1分
S=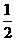 t2-2t(t>4)
t2-2t(t>4) ……… 1分
……… 1分
当CR∥AB时,t=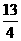 , S=
, S=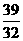 ……… 1分
……… 1分
当AR∥BC时,t= , S=
, S=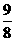 ……… 1分
……… 1分
当BR∥AC时,t=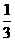 , S=
, S=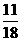 ……… 1分
……… 1分
3、如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q。
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断⊿BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由。
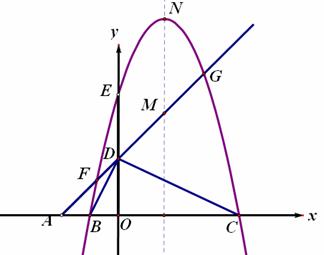
解:(1)B(-1,0) E(0,4) C(4,0) 设解析式是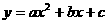
可得 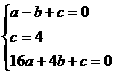 解得
解得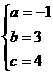 (2分)
∴
(2分)
∴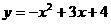 (1分)
(1分)
(2)⊿BDC是直角三角形 (1分)
∵BD2=BO2+DO2=5 , DC2=DO2+CO2=20 ,BC2=(BO+CO)2=25
∴BD2+ DC2= BC2 (1分)
∴⊿BDC是Rt⊿
点A坐标是(-2,0),点D坐标是(0,2)直线AD的解析式是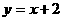 (1分)
(1分)
设点P坐标是(x,x+2)
当OP=OC时 x2+(x+2)2=16 解得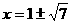 (
(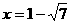 不符合,舍去)此时点P(
不符合,舍去)此时点P(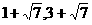 )
)
当PC=OC时 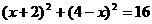 方程无解
方程无解
当PO=PC时,点P在OC的中垂线上,∴点P横坐标是2, 得点P坐标是(2,4)
∴当⊿POC是等腰三角形时,点P坐标是(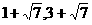 )或(2,4) (2分)
)或(2,4) (2分)
(1) 点M坐标是(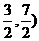 )N坐标是(
)N坐标是(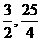 )∴MN=
)∴MN=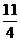
设点P 为(x,x+2)Q(x,-x2+3x+4),则PQ=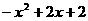
①若PQNM是菱形,则PQ=MN,可得x1=0.5 x2=1.5
当x2=1.5时,点P与点M重合;当x1=0.5时,可求得PM=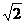 ,所以菱形不存在(2分)
,所以菱形不存在(2分)
②能成为等腰梯形,此时点P的坐标是(2.5,4.5)(2分)
2、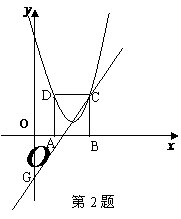 如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=
如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=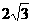 ,直线y=
,直线y=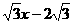 经过点C,交y轴于点G。
经过点C,交y轴于点G。
(1)点C、D的坐标分别是C( ),D( );
(2)求顶点在直线y=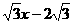 上且经过点C、D的抛物
上且经过点C、D的抛物
线的解析式;
(3)将(2)中的抛物线沿直线y=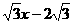 平移,平移后
平移,平移后
的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。
平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?
若存在,请求出此时抛物线的解析式;若不存在,请说
明理由。
解:(1)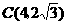
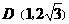
|
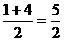 ,代入一次函数
,代入一次函数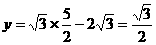 ,得顶点坐标为(
,得顶点坐标为(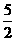 ,
,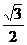 ),
),
∴设抛物线解析式为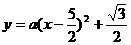 ,把点
,把点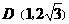 代入得,
代入得,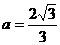
|
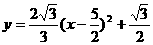
(3)设顶点E在直线上运动的横坐标为m,则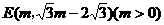
|
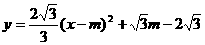
①当FG=EG时,FG=EG=2m,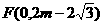 代入解析式得:
代入解析式得:
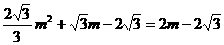 ,得m=0(舍去),
,得m=0(舍去),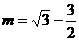 ,
,
|
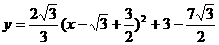 ;
;
②当GE=EF时,FG=4m,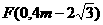 代入解析式得:
代入解析式得:
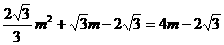 ,得m=0(舍去),
,得m=0(舍去),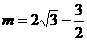 ,
,
|
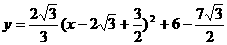 ;
;
③当FG=FE时,不存在;
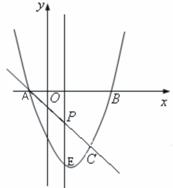
1、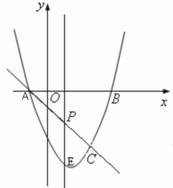 如图,抛物线
如图,抛物线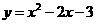 与x轴交A、B两点(A点在B点左侧),直线
与x轴交A、B两点(A点在B点左侧),直线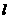 与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B 两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交
抛物线于E点,求线段PE长度的最大值;
(3)点G是抛物线上的动点,在x轴上是否存在点F,
使A、C、F、G这样的四个点为顶点的四边形是
平行四边形?如果存在,直接写出所有满足条件的F
点坐标;如果不存在,请说明理由.
解:(1)令y=0,解得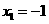 或
或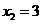
∴A(-1,0)B(3,0); (2分)
 将C点的横坐标x=2代入
将C点的横坐标x=2代入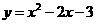 得y=-3,∴C(2,-3)(1分)
得y=-3,∴C(2,-3)(1分)
∴直线AC的函数解析式是y=-x-1 (1分)
(2)设P点的横坐标为x(-1≤x≤2)(注:x的范围不写不扣分)
则P、E的坐标分别为:P(x,-x-1),
E(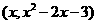
∵P点在E点的上方,PE=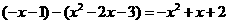 (2分)
(2分)
=-(x-1/2)2+9/4 (1分)
∴当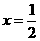 时,PE的最大值=
时,PE的最大值=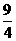 (1分)
(1分)
(3) 存在4个这样的点F,分别是
F1(1,0) F2(-3,0) F3(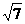 +4 ,0) F4(-
+4 ,0) F4(-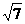 +4 ,0)(共4分,对1个得1分)
+4 ,0)(共4分,对1个得1分)
3、如图,已知⊙O与⊙P相交于A、B两点,点P在⊙O上,⊙O的弦AC切⊙P于点A,CP及其延长线交⊙P于D、E,过点E作EF⊥CE交CB的延长线于F。
(1)求证:BC是⊙P的切线;
(2)若CD=2,CB=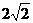 ,求EF的长;
,求EF的长;
(3)若设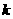 =PE∶CE,是否存在实数
=PE∶CE,是否存在实数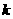 ,使△PBD恰好是等边三角形?若存在,求出
,使△PBD恰好是等边三角形?若存在,求出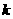 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com