
题目列表(包括答案和解析)
7、(2011•滨州)抛物线y=(x+2)2﹣3可以由抛物线y=x2平移得到,则下列平移过程正确的是( )
A、先向左平移2个单位,再向上平移3个单位 B、先向左平移2个单位,再向下平移3个单位
C、先向右平移2个单位,再向下平移3个单位 D、先向右平移2个单位,再向上平移3个单位
考点:二次函数图象与几何变换。
专题:探究型。
分析:根据“左加右减,上加下减”的原则进行解答即可.
解答:解:抛物线y=x2向左平移2个单位可得到抛物线y=(x+2)2,
抛物线y=(x+2)2,再向下平移3个单位即可得到抛物线y=(x+2)2﹣3.
故平移过程为:先向左平移2个单位,再向下平移3个单位.
故选B.
点评:本题考查的是二次函数的图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.
6、(2011•滨州)关于一次函数y=﹣x+1的图象,下列所画正确的是( )
A、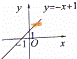 B、
B、
C、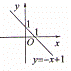 D、
D、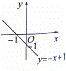
考点:一次函数的图象。
专题:常规题型。
分析:根据函数的k为﹣1,b=1,可判断函数为减函数,且与y轴的交点在y轴的负半轴.
解答:解:由题意得:函数的k为﹣1,b=1,
∴函数为减函数,且与y轴的交点在y轴的负半轴,
结合选项可得C符合题意.
故选C.
点评:本题考查一次函数的图象的知识,难度不大,对于此类题目要先判断增减性及与y轴交点的位置.
5、(2011•滨州)若某三角形的两边长分别为3和4,则下列长度的线段能作为其第三边的是( )
A、1 B、5
C、7 D、9
考点:三角形三边关系。
专题:应用题。
分析:此题首先根据三角形的三边关系,求得第三边的取值范围,再进一步找到符合条件的数值.
解答:解:根据三角形的三边关系,得:第三边应>两边之差,即4﹣3=1,而<两边之和,即4+3=7,
即1<第三边<7,
∴只有5符合条件,
故选B.
点评:本题主要考查了构成三角形的条件:两边之和>第三边,两边之差<第三边,比较简单.
4、(2011•滨州)四张质地、大小、背面完全相同的卡片上,正面分别画有圆、矩形、等边三角形、等腰梯形四个图案.现把它们的正面向下随机摆放在桌面上,从中任意抽出一张,则抽出的卡片正面图案是中心对称图形的概率为( )
A、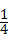 B、
B、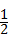
C、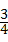 D、1
D、1
考点:概率公式;中心对称图形。
专题:计算题。
分析:先判断出圆、矩形、等边三角形、等腰梯形中的中心对称图形,再根据概率公式解答即可.
解答:解:圆、矩形、等边三角形、等腰梯形中,中心对称图形有圆,矩形2个;
则P(中心对称图形)=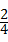 =
=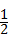 .
.
故选B.
点评:此题考查了概率公式和中心对称图形的定义,要弄清概率公式适用的条件方可解题:
(1)试验中所有可能出现的基本事件有有限个;
(2)每个基本事件出现的可能性相等.
3、(2008•衢州)某商品原价289元,经连续两次降价后售价为256元,设平均每降价的百分率为x,则下面所列方程正确的是( )
A、289(1﹣x)2=256 B、256(1﹣x)2=289
C、289(1﹣2x)2=256 D、256(1﹣2x)2=289
考点:由实际问题抽象出一元二次方程。
专题:增长率问题。
分析:增长率问题,一般用增长后的量=增长前的量×(1+增长率),本题可参照增长率问题进行计算,如果设平均每次降价的百分率为x,可以用x表示两次降价后的售价,然后根据已知条件列出方程.
解答:解:根据题意可得两次降价后售价为289(1﹣x)2,
∴方程为289(1﹣x)2=256.
故选答A.
点评:本题考查一元二次方程的应用,解决此类两次变化问题,可利用公式a(1+x)2=c,其中a是变化前的原始量,c是两次变化后的量,x表示平均每次的增长率.
本题的主要错误是有部分学生没有仔细审题,把答题案错看成B.
2、二次根式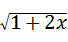 有意义时,x的取值范围是( )
有意义时,x的取值范围是( )
A、x≥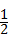 B、x≤﹣
B、x≤﹣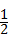
C、x≥﹣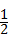 D、x≤
D、x≤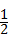
考点:二次根式有意义的条件;解一元一次不等式。
专题:存在型。
分析:根据二次根式的性质和分式的意义,被开方数大于等于0,列出不等式,求出x的取值范围即可.
解答:解:∵二次根式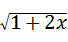 有意义,
有意义,
∴1+2x≥0,
解得x≥﹣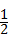 .
.
故选C.
点评:本题考查的是二次根式有意义的条件及解一元一次不等式,比较简单.
1、(2011•滨州)在实数π、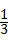 、
、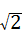 、sin30°,无理数的个数为( )
、sin30°,无理数的个数为( )
A、1 B、2
C、3 D、4
考点:无理数;特殊角的三角函数值。
专题:探究型。
分析:先把sin30°化为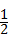 的形式,再根据无理数的定义进行解答即可.
的形式,再根据无理数的定义进行解答即可.
解答:解:∵sin30°=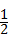 ,
,
∴这一组数中的无理数有:π,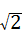 .
.
故选B.
点评:本题考查的是无理数的定义,即其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.
24.(本题满分l2分)
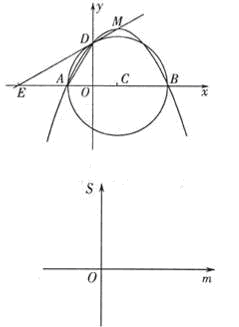 如图,y关于x的二次函数
如图,y关于x的二次函数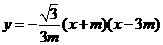 图象的顶点为M,图象交x轴于A.B两点.交y轴正半轴于D点.以AB为直径作圆,圆心为C。定点E的坐标为(
图象的顶点为M,图象交x轴于A.B两点.交y轴正半轴于D点.以AB为直径作圆,圆心为C。定点E的坐标为(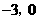 ),连接ED.(
),连接ED.(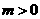 )
)
(1) 写出A、B、D三点的坐标;
(2) 当m为何值时,M点在直线ED上?判定此时直线ED与圆的位置关系;
(3) 当m变化时,甩m表示△AED的面积S.
并在给出的直角坐标系中画出S关于m的函数图象的示意图.




23.(本题满分11分)
如图.AB是半圆O的直径.AB=2.射线AM、BN为半圆O的切线.在AM上取一点D.连接BD交半圆于点C.连接AC,过O点作BC的垂线OF.垂足为点E.与BN相交于点F。过D点作半圆O的切线DP,切点为P,与BN相交于点 Q。
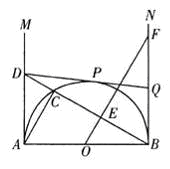 (I) 求证:△ABC'∽△OFB;
(I) 求证:△ABC'∽△OFB;
(2) 当△ABD与△BFO的面积相等时,求BQ的长;
(3) 求证:当D在AM上移动时(A点除外),点Q始终是线段BF的中点。
22.(本题满分l0分)
2010年上半年.某种农产品受不良炒作的影响.价格一路上扬.8月初国家实施调控措施后,该农产品的价格开始回落.其中,1月份至7月份.该农产品的月平均价格y元/千克与月份x呈一次函数关系;7月份至I2月份.月平均价格y元/千克与月份x呈二次函数关系.已知l月、7月、9月和l2月这四个月的月平均价格分别为8元/千克、26元/千克、l4元/千克、11元/千克.
(1) 分别求出当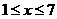 和
和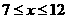 时.y关于x的函数关系式;
时.y关于x的函数关系式;
(2) 2010年的l2个月中.这种农产品的月平均价格哪个月最低?最低为多少?
(3) 若以l2个月份的月平均价格的平均数为年平均价格.月平均价格高于年平均价格的月份有哪些?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com