
题目列表(包括答案和解析)
2、(2011•泰安)下列运算正确的是( )
A、3a2+4a2=7a4 B、3a2﹣4a2=﹣a2
C、3a•4a2=12a2 D、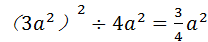
考点:整式的除法;合并同类项;单项式乘单项式。
专题:计算题。
分析:根据单项式除单项式的法则、合并同类项以及整式的除法法则计算即可.
解答:解:A、3a2+4a2=7a2,故本选项错误;
B、3a2﹣4a2=﹣a2,故本选项正确;
C、3a•4a2=12a3,故本选项错误;
D、(3a2)2÷4a2=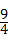 a2,故本选项错误;
a2,故本选项错误;
故选B.
点评:本题主要考查多项式除以单项式运算、合并同类项以及整式的除法法则,牢记法则是关键.
1、(2011•泰安)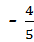 的倒数是( )
的倒数是( )
A、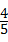 B、
B、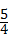
C、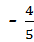 D、
D、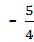
考点:倒数。
专题:计算题。
分析:根据倒数的定义:乘积是1的两数互为倒数.
一般地,a•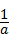 =1 (a≠0),就说a(a≠0)的倒数是
=1 (a≠0),就说a(a≠0)的倒数是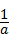 .
.
解答:解: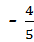 的倒数是﹣
的倒数是﹣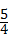 ,
,
故选D.
点评:此题主要考查倒数的概念及性质.倒数的定义:若两个数的乘积是1,我们就称这两个数互为倒数.
25、(2011•滨州)如图,某广场设计的一建筑物造型的纵截面是抛物线的一部分,抛物线的顶点O落在水平面上,对称轴是水平线OC.点A、B在抛物线造型上,且点A到水平面的距离AC=4米,点B到水平面距离为2米,OC=8米.
(1)请建立适当的直角坐标系,求抛物线的函数解析式;
(2)为了安全美观,现需在水平线OC上找一点P,用质地、规格已确定的圆形钢管制作两根支柱PA、PB对抛物线造型进行支撑加固,那么怎样才能找到两根支柱用料最省(支柱与地面、造型对接方式的用料多少问题暂不考虑)时的点P?(无需证明)
(3)为了施工方便,现需计算出点O、P之间的距离,那么两根支柱用料最省时点O、P之间的距离是多少?(请写出求解过程)
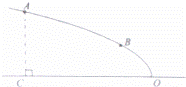
考点:二次函数的应用。
分析:(1)以点O为原点、射线OC为y轴的正半轴建立直角坐标系,可设抛物线的函数解析式为y=ax2,又由点A在抛物线上,即可求得此抛物线的函数解析式;
(2)延长AC,交建筑物造型所在抛物线于点D,连接BD交OC于点P,则点P即为所求;
(3)首先根据题意求得点B与D的坐标,设直线BD的函数解析式为y=kx+b,利用待定系数法即可求得直线BD的函数解析式,把x=0代入y=﹣x+4,即可求得点P的坐标.
解答:解:(1)以点O为原点、射线OC为y轴的正半轴建立直角坐标系,
设抛物线的函数解析式为y=ax2,
由题意知点A的坐标为(4,8).
∵点A在抛物线上,
∴8=a×42,
解得a=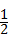 ,
,
∴所求抛物线的函数解析式为:y=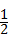 x2;
x2;
(2)找法:
延长AC,交建筑物造型所在抛物线于点D,
则点A、D关于OC对称.
连接BD交OC于点P,则点P即为所求.
(3)由题意知点B的横坐标为2,
∵点B在抛物线上,
∴点B的坐标为(2,2),
又∵点A的坐标为(4,8),
∴点D的坐标为(﹣4,8),
设直线BD的函数解析式为y=kx+b,
∴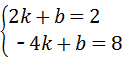 ,
,
解得:k=﹣1,b=4.
∴直线BD的函数解析式为y=﹣x+4,
把x=0代入y=﹣x+4,得点P的坐标为(0,4),
两根支柱用料最省时,点O、P之间的距离是4米.
点评:此题考查了二次函数的实际应用问题.解此题的关键是根据题意构建二次函数模型,然后根据二次函数解题.
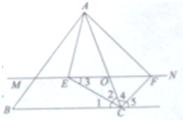
24、(2011•滨州)如图,在△ABC中,点O是AC边上(端点除外)的一个动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,连接AE、AF.那么当点O运动到何处时,四边形AECF是矩形?并证明你的结论.

考点:矩形的判定。
专题:证明题。
分析:当点O运动到AC的中点(或OA=OC)时,四边形AECF是矩形.由于CE平分∠BAC,那么有∠1=∠2,而MN∥BC,利用平行线的性质有∠1=∠3,等量代换有∠2=∠3,于OE=OC,同理OC=OF,于是OE=OF,而OA=OC,那么可证四边形AECF是平行四边形,又CE、CF分别是∠BCA及其外角的平分线,易证∠ECF是90°,从而可证四边形AECF是矩形.
解答:当点O运动到AC的中点(或OA=OC)时,四边形AECF是矩形.
证明:∵CE平分∠BCA,
∴∠1=∠2,
又∵MN∥BC,
∴∠1=∠3,
∴∠3=∠2,
∴EO=CO,
同理,FO=CO,
∴EO=FO,
又∵OA=OC,
∴四边形AECF是平行四边形,
又∵∠1=∠2,∠4=∠5,
∴∠1+∠5=∠2+∠4,
又∵∠1+∠5+∠2+∠4=180°,
∴∠2+∠4=90°,
∴四边形AECF是矩形.
点评:本题考查了角平分线的性质、平行线的性质、平行四边形的判定、矩形的判定.解题的关键是利用对角线互相平分的四边形是平行四边形开证明四边形AECF是平行四边形,并证明∠ECF是90°.
23、(2011•滨州)根据给出的下列两种情况,请用直尺和圆规找到一条直线,把△ABC恰好分割成两个等腰三角形(不写做法,但需保留作图痕迹);并根据每种情况分别猜想:∠A与∠B有怎样的数量关系时才能完成以上作图?并举例验证猜想所得结论.
(1)如图①△ABC中,∠C=90°,∠A=24°
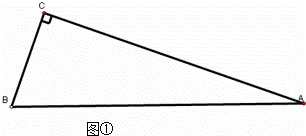
①作图:
②猜想:
③验证:
(2)如图②△ABC中,∠C=84°,∠A=24°.
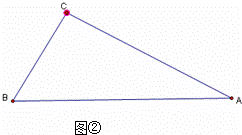
①作图:
②猜想:
③验证:
考点:作图-复杂作图。
分析:(1)①痕迹能体现作线段AB(或AC、或BC)的垂直平分线,或作∠ACD=∠A(或∠BCD=∠B)两类方法均可,
②利用各角之间的关系得出∠A+∠B=90°;
③可根据△ABC中,∠A=30°,∠B=60°时,有∠A+∠B=90°,此时就能找到一条把△ABC恰好分割成两个等腰三角形的直线.
(2)①痕迹能体现作线段AB(或AC、或BC)的垂直平分线,或作∠ACD=∠A或在线段CA上截取CD=CB三种方法均可.
②利用各角之间的关系得出∠B=3∠A;
③利用特殊角∠A=32°,∠B=96,有∠B=3∠A,此时就能找到一条把△ABC恰好分割成两个等腰三角形的直线.
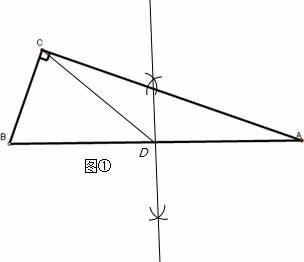
解答:解:(1)①作图:痕迹能体现作线段AB(或AC、或BC)的垂直平分线,或作∠ACD=∠A(或∠BCD=∠B)两类方法均可,
在边AB上找出所需要的点D,则直线CD即为所求(2分)
②猜想:∠A+∠B=90°,(4分)
③验证:如在△ABC中,∠A=30°,∠B=60°时,有∠A+∠B=90°,此时就能找到一条把△ABC恰好分割成两个等腰三角形的直线.(5分)
(2)答:①作图:痕迹能体现作线段AB(或AC、或BC)的垂直平分线,或作∠ACD=∠A或在线段CA上截取CD=CB三种方法均可.
在边AB上找出所需要的点D,则直线CD即为所求(6分)
②猜想:∠B=3∠A(8分)
③验证:如在△ABC中,∠A=32°,∠B=96,有∠B=3∠A,此时就能找到一条把△ABC恰好分割成两个等腰三角形的直线.(9分).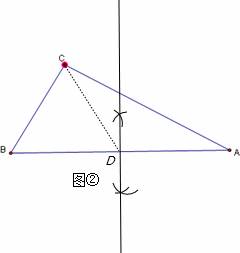
点评:此题主要考查了垂直平分线的作法以及垂直平分线的性质和三角形内角和定理的应用,根据垂直平分线的性质作出图形是解决问题的关键.
22、(2011•滨州)如图,直线PM切⊙O于点M,直线PO交⊙O于A、B两点,弦AC∥PM,连接OM、BC.
求证:(1)△ABC∽△POM;(2)2OA2=OP•BC.
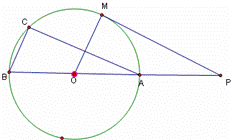
考点:切线的性质;相似三角形的判定与性质。
分析:(1)因为PM切⊙O于点M,所以∠PMO=90°,又因为弦AB是直径,所以∠ACB=∠PMO=90°,再有条件弦AC∥PM,可证得∠CAB=∠P,进而可证得△ABC∽△POM;
(2)有(1)可得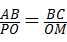 ,又因为AB=2OA,OA=OM;所以2OA2=OP•BC.
,又因为AB=2OA,OA=OM;所以2OA2=OP•BC.
解答:证明:(1)∵直线PM切⊙O于点M,
∴∠PMO=90°,
∵弦AB是直径,
∴∠ACB=90°,
∴∠ACB=∠PMO,
∵AC∥PM,
∴∠CAB=∠P,
∴△ABC∽△POM;
(2)∵△ABC∽△POM,
∴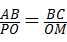 ,
,
又AB=2OA,OA=OM,
∴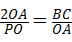 ,
,
∴2OA2=OP•BC.
点评:本题考查了切线的性质:①圆的切线垂直于经过切点的半径;②经过圆心且垂直于切线的直线必经过切点;③经过切点且垂直于切线的直线必经过圆心和相似和圆有关的知识,具有一定的综合性.
21、(2011•滨州)甲、乙两名同学进行射击训练,在相同条件下各射靶5次,成绩统计如下:
|
命中环数 |
7 |
8 |
9 |
10 |
|
甲命中相应环数的次数 |
2 |
2 |
0 |
1 |
|
乙命中相应环数的次数 |
1 |
3 |
1 |
0 |
若从甲、乙两人射击成绩方差的角度评价两人的射击水平,则谁的射击成绩更稳定些?
考点:方差。
专题:计算题。
分析:根据平均数的公式:平均数=所有数之和再除以数的个数;方差就是各变量值与其均值离差平方的平均数,根据方差公式计算即可,所以计算方差前要先算出平均数,然后再利用方差公式计算.
解答:解:甲、乙两人射击成绩的平均成绩分别为: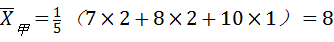 ,(2分)
,(2分)
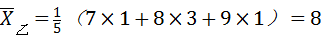 ,(3分)
,(3分)
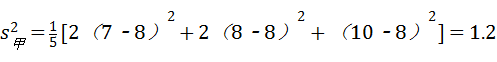 ,(5分)
,(5分)
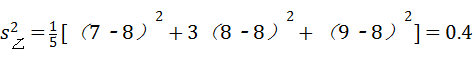 ,(6分)
,(6分)
∵s甲2<s乙2.
∴乙同学的射击成绩比较稳定.(8分).
点评:本题考查平均数、方差的定义:一般地设n个数据,x1,x2,…xn的平均数为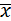 ,则方差S2=
,则方差S2=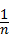 [(x1﹣
[(x1﹣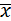 )2+(x2﹣
)2+(x2﹣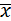 )2+…+(xn﹣
)2+…+(xn﹣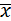 )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
平均数反映了一组数据的集中程度,求平均数的方法是所有数之和再除以数的个数;
方差是各变量值与其均值离差平方的平均数,它是测算数值型数据离散程度的最重要的方法.
20、(2011•滨州)依据下列解方程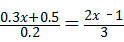 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
解:原方程可变形为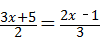 ( 分式的基本性质 )
( 分式的基本性质 )
去分母,得3(3x+5)=2(2x﹣1).( 等式性质2 )
去括号,得9x+15=4x﹣2.( 去括号法则或乘法分配律 )
( 移项 ),得9x﹣4x=﹣15﹣2.( 等式性质1 )
合并,得5x=﹣17.( 合并同类项 )
( 系数化为1 ),得x=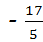 .( 等式性质2 )
.( 等式性质2 )
考点:解一元一次方程。
分析:解方程要先去分母,去括号,移项合并同类项,系数化1,最后求得解.
解答:解:原方程可变形为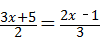 (分式的基本性质)
(分式的基本性质)
去分母,得3(3x+5)=2(2x﹣1).(等式性质2)
去括号,得9x+15=4x﹣2.(去括号法则或乘法分配律)
(移项),得9x﹣4x=﹣15﹣2.(等式性质1)
合并,得5x=﹣17.(合并同类项)
(系数化为1),得x=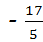 .(等式性质2)
.(等式性质2)
点评:本题考查解一元一次方程,关键知道解一元一次方程常见的过程有去分母,去括号、移项、系数化为1,最后得解.
19、(2011•滨州)计算: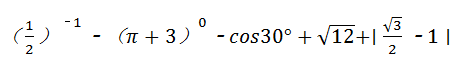 .
.
考点:实数的运算;零指数幂;负整数指数幂。
专题:计算题。
分析:本题涉及零指数幂、负指数幂、特殊角的三角函数、绝对值、二次根式化简5个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
解答:解:原式=2﹣1﹣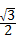 +2
+2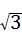 +1﹣
+1﹣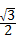
=2+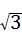 .
.
点评:本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、特殊角的三角函数值、绝对值等考点的运算
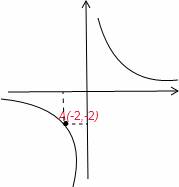
18、(2011•滨州)若点A(m,﹣2)在反比例函数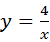 的图象上,则当函数值y≥﹣2时,自变量x的取值范围是 x≤﹣2或x>0 .
的图象上,则当函数值y≥﹣2时,自变量x的取值范围是 x≤﹣2或x>0 .
考点:反比例函数的性质。
分析:根据题意可求点A的坐标;画出草图,运用观察法求解.
解答:解:∵点A(m,﹣2)在反比例函数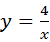 的图象上,
的图象上,
∴﹣2m=4,m=﹣2.
∴A(﹣2,﹣2).
∴当函数值y≥﹣2时,自变量x的取值范围是 x≤﹣2或x>0.
故答案为:x≤﹣2或x>0.
点评:此题考查了反比例函数的图象及其性质以及运用观察法解不等式,难度中等.注意反比例函数的图象是双曲线.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com