
题目列表(包括答案和解析)
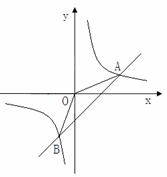
20.(2011重庆綦江,23,10分)如图,已知A(4,a),B(-2,-4)是一次函数y=kx+b的图象和反比例函数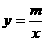 的图象的交点.
的图象的交点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.
[答案]:解: (1)将B(-2,-4)代入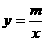 ,解得 m=8 ∴反比例函数的解析式为
,解得 m=8 ∴反比例函数的解析式为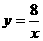 ,又∵点A在
,又∵点A在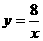 图象上,∴a=2 即点A坐标为(4,2)
图象上,∴a=2 即点A坐标为(4,2)
将A(4,2); B(-2,-4)代入y=kx+b得
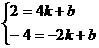 解得
解得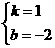
∴一次函数的解析式为y=x-2
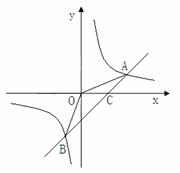
(2)设直线与x轴相交于点C,则C点的坐标为(2,0)
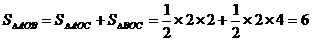 (平方单位)
(平方单位)
注:若设直线与y轴相交于点D,求出D点坐标(0,-2),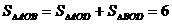 (平方单位)同样给分.
(平方单位)同样给分.
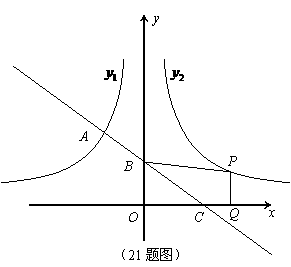
19. (2011四川宜宾,21,7分)如图,一次函数的图象与反比例函数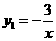 (x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),当x<-1时,一次函数值大于反比例函数值,当x>-1时,一次函数值小于反比例函数值.
(x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0),当x<-1时,一次函数值大于反比例函数值,当x>-1时,一次函数值小于反比例函数值.
(1)求一次函数的解析式;
(2)设函数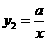 (x>0)的图象与
(x>0)的图象与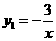 (x<0)的图象关于y轴对称,在
(x<0)的图象关于y轴对称,在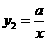 (x>0)的图象上取一点P(P点的横坐标大于2),过P点作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
(x>0)的图象上取一点P(P点的横坐标大于2),过P点作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.

[答案]解:⑴∵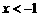 时,一次函数值大于反比例函数值,当
时,一次函数值大于反比例函数值,当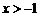 时,一次函数值小于反比例函数值.
时,一次函数值小于反比例函数值.
∴A点的横坐标是-1,∴A(-1,3)
设一次函数解析式为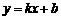 ,因直线过A、C
,因直线过A、C
则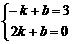 解得
解得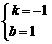
∴一次函数的解析式为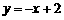 .
.
⑵∵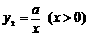 的图象与
的图象与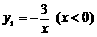 的图象关于y轴对称,
的图象关于y轴对称,
∴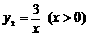
∵B点是直线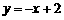 与y轴的交点,∴B(0,2)
与y轴的交点,∴B(0,2)
设P(n,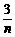 ),
),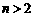 ,S四边形BCQP=S梯形BOQP-S△BOC=2
,S四边形BCQP=S梯形BOQP-S△BOC=2
∴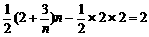 ,
,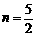 ,
,
∴P(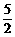 ,
,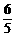 )
)
18. (2011四川内江,21,10分)如图,正比例函数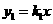 与反比例函数
与反比例函数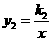 相交于A、B点,已知点A的坐标为(4,n),BD⊥x轴于点D,且S△BDO=4。过点A的一次函数
相交于A、B点,已知点A的坐标为(4,n),BD⊥x轴于点D,且S△BDO=4。过点A的一次函数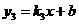 与反比例函数的图像交于另一点C,与x轴交于点E(5,0)。
与反比例函数的图像交于另一点C,与x轴交于点E(5,0)。
(1)求正比例函数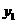 、反比例函数
、反比例函数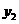 和一次函数
和一次函数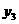 的解析式;
的解析式;
(2)结合图像,求出当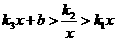 时x的取值范围。
时x的取值范围。
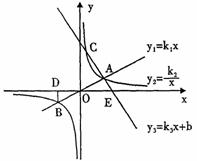
[答案](1)设B(p,q),则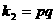
又S△BDO=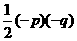 =4,得
=4,得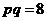 ,所以
,所以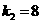 ,所以
,所以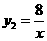
得A(4,2) ,得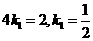 ,所以
,所以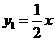
由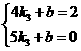 得
得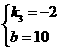 ,所以
,所以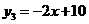
(2)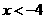 或
或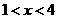
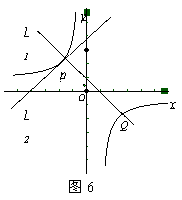
17. (2011四川广安,24,8分)如图6所示,直线l1的方程为y=-x+l,直线l2的方程为y=x+5,且两直线相交于点P,过点P的双曲线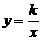 与直线l1的另一交点为Q(3.M).
与直线l1的另一交点为Q(3.M).
(1)求双曲线的解析式.
(2)根据图象直接写出不等式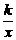 >-x+l的解集.
>-x+l的解集.

[答案]解:(1)依题意: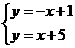
解得: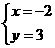
∴双曲线的解析式为:y=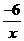
(2)-2<x<0或x>3
16. (2011四川成都,19,10分) 如图,已知反比例函数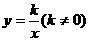 的图象经过点(
的图象经过点(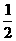 ,8),直线
,8),直线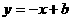 经过该反比例函数图象上的点Q(4,
经过该反比例函数图象上的点Q(4, ).
).
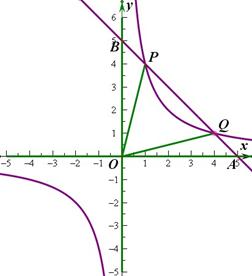
(1)求上述反比例函数和直线的函数表达式;
(2)设该直线与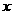 轴、
轴、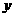 轴分别相交于A 、B两点,与反比例函数图象的另一个交点为P,连结0P、OQ,求△OPQ的面积.
轴分别相交于A 、B两点,与反比例函数图象的另一个交点为P,连结0P、OQ,求△OPQ的面积.
[答案]解:(1)由反比例函数的图象经过点(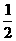 ,8),可知
,8),可知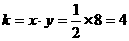 ,所以反比例函数解析式为
,所以反比例函数解析式为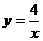 ,∵点Q是反比例函数和直线
,∵点Q是反比例函数和直线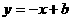 的交点,∴
的交点,∴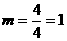 ,∴点Q的坐标是(4,1),∴
,∴点Q的坐标是(4,1),∴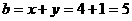 ,∴直线的解析式为
,∴直线的解析式为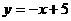 .
.
(2)如图所示:由直线的解析式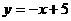 可知与
可知与 轴和
轴和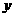 轴交点坐标点A与点B的坐标分别为(5,0)、(0,5),由反比例函数与直线的解析式可知两图像的交点坐标分别点P(1,4)和点Q(4,1),过点P作PC⊥
轴交点坐标点A与点B的坐标分别为(5,0)、(0,5),由反比例函数与直线的解析式可知两图像的交点坐标分别点P(1,4)和点Q(4,1),过点P作PC⊥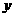 轴,垂足为C,过点Q作QD⊥
轴,垂足为C,过点Q作QD⊥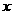 轴,垂足为D,
轴,垂足为D,
∴S△OPQ=S△AOB-S△OAQ-S△OBP =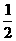 ×OA×OB-
×OA×OB-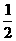 ×OA×QD-
×OA×QD-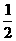 ×OB×PC
×OB×PC
=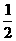 ×25-
×25-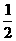 ×5×1-
×5×1-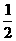 ×5×1=
×5×1=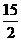 .
.
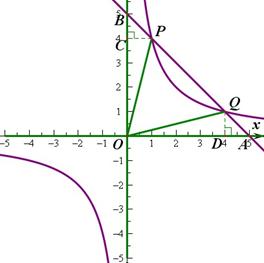
15. (2011山东聊城,24,10分)如图,已知一次函数y=kx+b的图象交反比例函数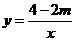 (x>0)图象于点A、B,交x轴于点C.
(x>0)图象于点A、B,交x轴于点C.
(1)求m的取值范围;
(2)若点A的坐标是(2,-4),且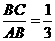 ,求m的值和一次函数的解析式;
,求m的值和一次函数的解析式;
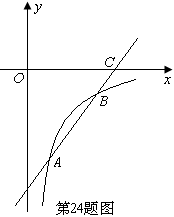
[答案](1)因反比例函数的图象在第四象限,所以4-2m<0,解得m>2;(2)因点A(2,-4)在反比例函数图象上,所以-4=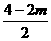 ,解得m=6,过点A、B分别作AM⊥OC于点M,BN⊥OC于点N,所以∠BNC=∠AMC=90°,又因为∠BCN=∠AMC,所以△BCN∽△ACM,所以
,解得m=6,过点A、B分别作AM⊥OC于点M,BN⊥OC于点N,所以∠BNC=∠AMC=90°,又因为∠BCN=∠AMC,所以△BCN∽△ACM,所以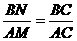 ,因为
,因为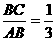 ,所以
,所以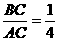 ,即
,即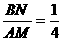 ,因为AM=4,所以BN=1,所以点B的纵坐标为-1,因为点B在反比例函数的图象上,所以当y=-1时,x=8,所以点B的坐标为(8,-1),因为一次函数y=kx+b的图象过点A(2,-4),B(8,-1),所以
,因为AM=4,所以BN=1,所以点B的纵坐标为-1,因为点B在反比例函数的图象上,所以当y=-1时,x=8,所以点B的坐标为(8,-1),因为一次函数y=kx+b的图象过点A(2,-4),B(8,-1),所以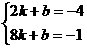 ,解得
,解得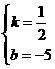 ,所以一次函数的解析式为y=
,所以一次函数的解析式为y=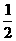 x-5
x-5
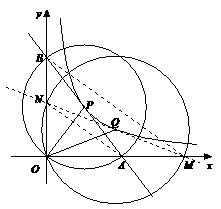
14. (2011江苏宿迁,26,10分)如图,在平面直角坐标系中,O为坐标原点,P是反比例函数y=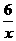 (x>0)图象上的任意一点,以P为圆心,PO为半径的圆与x、y轴分别交于点A、B.
(x>0)图象上的任意一点,以P为圆心,PO为半径的圆与x、y轴分别交于点A、B.
(1)判断P是否在线段AB上,并说明理由;
(2)求△AOB的面积;
(3)Q是反比例函数y=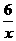 (x>0)图象上异于点P的另一点,请以Q为圆心,QO
(x>0)图象上异于点P的另一点,请以Q为圆心,QO
半径画圆与x、y轴分别交于点M、N,连接AN、MB.求证:AN∥MB.
[答案]
解:(1)点P在线段AB上,理由如下:
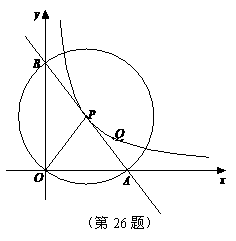
 ∵点O在⊙P上,且∠AOB=90°
∵点O在⊙P上,且∠AOB=90°
∴AB是⊙P的直径
∴点P在线段AB上.
(2)过点P作PP1⊥x轴,PP2⊥y轴,由题意可知PP1、PP2
是△AOB的中位线,故S△AOB=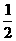 OA×OB=
OA×OB=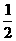 ×2
PP1×PP2
×2
PP1×PP2
∵P是反比例函数y=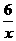 (x>0)图象上的任意一点
(x>0)图象上的任意一点
∴S△AOB=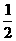 OA×OB=
OA×OB=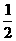 ×2
PP1×2PP2=2 PP1×PP2=12.
×2
PP1×2PP2=2 PP1×PP2=12.
(3)如图,连接MN,则MN过点Q,且S△MON=S△AOB=12.
∴OA·OB=OM·ON
∴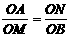
∵∠AON=∠MOB
∴△AON∽△MOB
∴∠OAN=∠OMB
∴AN∥MB.
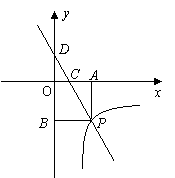
13. (2011甘肃兰州,24,7分)如图,一次函数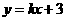 的图象与反比例函数
的图象与反比例函数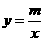 (x>0)的图象交于点P,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C、点D,且S△DBP=27,
(x>0)的图象交于点P,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C、点D,且S△DBP=27,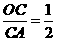 。
。
(1)求点D的坐标;
(2)求一次函数与反比例函数的表达式;
(3)根据图象写出当x取何值时,一次函数的值小于反比例函数的值?

[答案](1)D(0,3)
(2)设P(a,b),则OA=a,OC=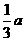 ,得C(
,得C(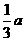 ,0)
,0)
因点C在直线y=kx+3上,得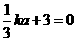 ,ka=-9
,ka=-9
DB=3-b=3-(ka+3)=-ka=9,BP=a
由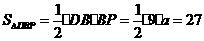 得a=6,所以
得a=6,所以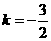 ,b=-6,m=-36
,b=-6,m=-36
一次函数的表达式为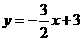 ,反比例函数的表达式为
,反比例函数的表达式为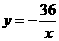
(3)x>6
12. (2011江西,19,6分)如图,四边形ABCD为菱形,已知A(0,4),B(-3,0)。
⑴求点D的坐标;
⑵求经过点C的反比例函数解析式.
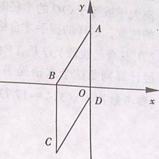
[答案](1)根据题意得AO=4,BO=3,∠AOB=90°,
所以AB=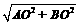 =
=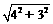 =5.
=5.
因为四边形ABCD为菱形,所以AD=AB=5,
所以OD=AD-AO=1,
因为点D在y轴负半轴,所以点D的坐标为(-1,0).
(2)设反比例函数解析式为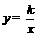 .
.
因为BC=AB=5,OB=3,
所以点C的坐标为(-3,-5).
因为反比例函数解析式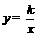 经过点C,
经过点C,
所以反比例函数解析式为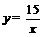 .
.
11. (2011浙江省嘉兴,19,8分)如图,已知直线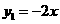 经过点P(
经过点P(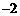 ,
,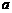 ),点P关于
),点P关于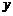 轴的对称点P′在反比例函数
轴的对称点P′在反比例函数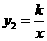 (
(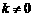 )的图象上.
)的图象上.
(1)求点P′的坐标;
(2)求反比例函数的解析式,并直接写出当y2<2时自变量x的取值范围.


[答案](1)将P(-2,a)代入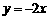 得a=-2×(-2)=4,∴P′(2,4).
得a=-2×(-2)=4,∴P′(2,4).
(2) 将P′(2,4)代入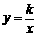 得4=
得4=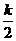 ,解得k=8,∴反比例函数的解析式为
,解得k=8,∴反比例函数的解析式为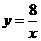 .
.
自变量x的取值范围x<0或x>4.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com