
题目列表(包括答案和解析)
7.设双曲线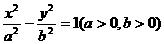 的右准线与两渐近线交于A、B两点,点F为右焦点,
的右准线与两渐近线交于A、B两点,点F为右焦点,
若以AB为直径的圆经过点F,则该双曲线的离心率为 ( )
A.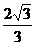 B.2 C.
B.2 C.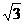 D.
D.
6.设曲线y=和曲线y=在它们交点处的两切线的夹角为θ,则tanθ= ( ) A.1 B. C. D.
5.复平面内点Z1、Z2对应复数分别为z1 z2 若|z1-z2|=|z1+z2|(z1z2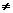 0)则向量
0)则向量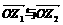 所成
所成
的角为 ( )
A.0° B.60° C.90° D.120°
4.函数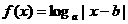 (
( ,且
,且 )是偶函数,且在
)是偶函数,且在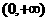 上单调递减,
上单调递减,
则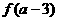 与
与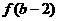 的大小关系是
( )
的大小关系是
( )
A.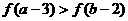 B.
B.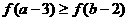
C.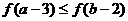 D.
D.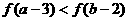
3.教室内有一直尺,无论怎样放置,在地面总有直线与直尺所在的直线 ( )
A.平行 B.垂直 C.相交 D.异面
2.若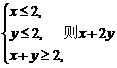 的取值范围是 ( )
的取值范围是 ( )
A.[2,6] B.[2,5] C.[3,6] D.[3,5]
只有一项是符合题目要求的)
1.函数 y=-x(x+2)(x≥0)的反函数定义域为 ( )
A. 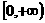 B.
B.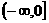 C. (0,1) D.
C. (0,1) D.
22.(本小题满分14分)
已知函数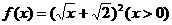 ,设正项数列{
,设正项数列{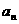 }的首项
}的首项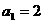 ,前n项和Sn满足
,前n项和Sn满足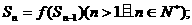
(1)求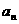 的表达式;
的表达式;
(2)在平面直角坐标系内,直线Ln的斜率为an,且Ln与曲线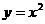 有且仅有一个公共点,Ln又与y轴交于点Dn(0,bn),当
有且仅有一个公共点,Ln又与y轴交于点Dn(0,bn),当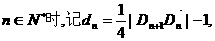
若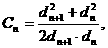 求证:C1+C2+C3…+Cn-n<1.
求证:C1+C2+C3…+Cn-n<1.
21. (本小题满分12分)已知点H(0,―3),点P在x轴上,点Q在y轴正半轴上,点M在直线PQ上,且满足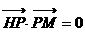 ,
,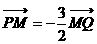 。
(1)当点P在x轴上移动时,求动点M的轨迹曲线C的方程;
(2)过定点A(a,b)的直线与曲线C相交于两点S、R,求证:抛物线S、R两点处的切线的交点B恒在一条直线上。
。
(1)当点P在x轴上移动时,求动点M的轨迹曲线C的方程;
(2)过定点A(a,b)的直线与曲线C相交于两点S、R,求证:抛物线S、R两点处的切线的交点B恒在一条直线上。
20.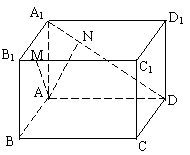 (本小题满分12分)如图,在长方体ABCD―A1B1C1D1中,AB=5,AD=8,AA1=
4,M为B1C1上一点,且B1M=2,点N在线段A1D上,A1D⊥AN,求:
(1)cos (
(本小题满分12分)如图,在长方体ABCD―A1B1C1D1中,AB=5,AD=8,AA1=
4,M为B1C1上一点,且B1M=2,点N在线段A1D上,A1D⊥AN,求:
(1)cos (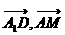 );
(2)直线AD与平面ANM所成的角的大小;
(3)平面ANM与平面ABCD所成角(锐角)的大小.
);
(2)直线AD与平面ANM所成的角的大小;
(3)平面ANM与平面ABCD所成角(锐角)的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com