
题目列表(包括答案和解析)
3.设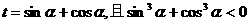 ,则t的取值范围是 ( )
,则t的取值范围是 ( )
(A)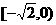 (B)
(B)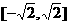
(C) (D)
(D)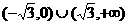
2.要使(log23)x-(log53)x≥(log53)-y-(log53)-y成立,则有 ( )
(A)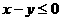 (B)
(B)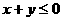 (C)
(C)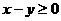 (D)
(D)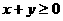
1.设双曲线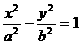 ,(a>0,b>0)的一条准线与两条渐近线交于A,B两点,相应焦点为
,(a>0,b>0)的一条准线与两条渐近线交于A,B两点,相应焦点为
F,若以AB为直径的圆过点F,则双曲线离心率为 ( )
(A) (B)
(B)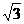 (C)2
(C)2  (D)
(D)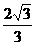
22.(14分)解:(1)抛物线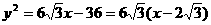 的项点为
的项点为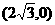 (文2理1分)
(文2理1分)
准线为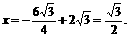 ……………………………(文4,理2分)
……………………………(文4,理2分)
设双曲线G为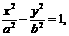 则有
则有 ,可得,a2=3,b2=9.
,可得,a2=3,b2=9.
∴双曲线G的方程为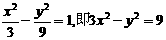 .……………………(文6,理4分)
.……………………(文6,理4分)
(2)①由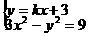 ,得
,得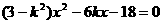 ………………………………(文7分)
………………………………(文7分)
又由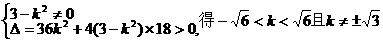 .………(文8,理5分)
.………(文8,理5分)
设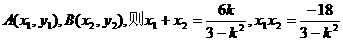 …………………………(文9分)
…………………………(文9分)
∵若原点O在AB为直径的圆上,有OA⊥OB,KOA·KOB=-1,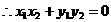 ,即
,即
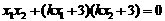 ……(文10,理6分) 化简为
……(文10,理6分) 化简为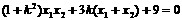
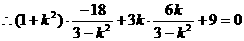 ………(文12,理7分)解得,
………(文12,理7分)解得,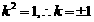 .
.
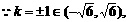 故,当k=±1时,原点O在AB为直径的圆上.………(文14,理8分)
故,当k=±1时,原点O在AB为直径的圆上.………(文14,理8分)
②设这样的实数k存在,则有
|
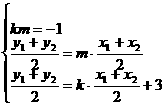
由②③得,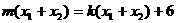 …………………………………………(12分)
…………………………………………(12分)
即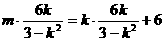 ,推得km=3,……………………………………(13分)
,推得km=3,……………………………………(13分)
这与km=-1矛盾,所以适合条件的k不存在.………………………(14分)
21.(12分)解:(1)等比数列的通项为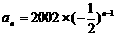 ……………………………2分
……………………………2分
前n项的积为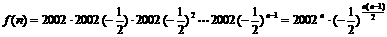 ………5分
………5分
(2)(文科)令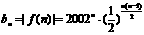 ,……6分
,……6分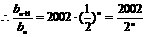 ………………8分
………………8分
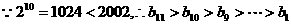 ,…………………………………………10分
,…………………………………………10分
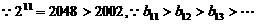 ,b11是最大值.
,b11是最大值.
故当n=11时,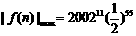 ……………………………12分
……………………………12分
(理科)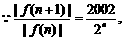 ………6分 ∴当
………6分 ∴当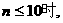
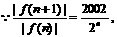 >1,
>1,
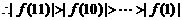 ……7分
当>10时,
……7分
当>10时,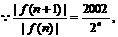 <1,
<1,
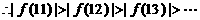 ,……………………………8分
,……………………………8分
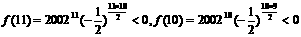
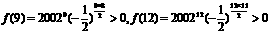 ……10分 故,只需比较f(9)与f(12)的
……10分 故,只需比较f(9)与f(12)的
大小就可以确定f(n)的最大值. 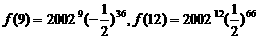
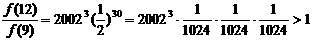 ………………11分
………………11分
故,n=12时,f(n)有最大值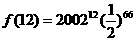 .…………………12分
.…………………12分
20.(12分)解:(文科)解:(1)依题意,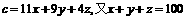
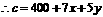 2分
2分
(2)由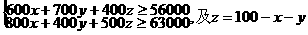 得,
得,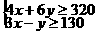 ,……4分
,……4分
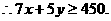 …………6分
…………6分 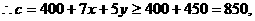 …………8分
…………8分
当且仅当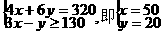 时等号成立.……………10分 ∴当x=50千克,y=20千克,
时等号成立.……………10分 ∴当x=50千克,y=20千克,
z=30千克时,混合物成本最低为850元.………………………………………12分
(理科)解(1)安全负荷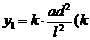 为正常数) 翻转
为正常数) 翻转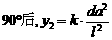 ………2分
………2分
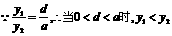 ,安全负荷变大.…4分当
,安全负荷变大.…4分当 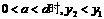 ,安全负荷变小. 6分
,安全负荷变小. 6分
 (2)如图,设截取的宽为a,高为d,则
(2)如图,设截取的宽为a,高为d,则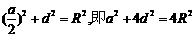 .
.
∵枕木长度不变,∴u=ad2最大时,安全负荷最大.
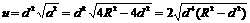 ……8分
……8分
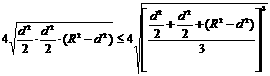
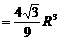 .………………………………………10分,当且仅当
.………………………………………10分,当且仅当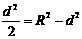 ,即取
,即取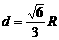 ,
,
取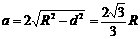 时,u最大, 即安全负荷最大.………………12分
时,u最大, 即安全负荷最大.………………12分
19.(12分)(1)证明:设 ,且
,且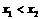 ,则
,则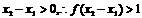 ……………2分
……………2分
而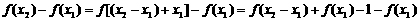 ………………4分
………………4分
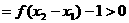 ∴
∴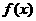 是增函数.……………………6分
是增函数.……………………6分
(2)解: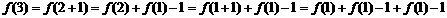
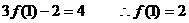 ……………8分
∴不等式即
……………8分
∴不等式即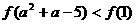 ,
,
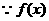 是增函数,∴
是增函数,∴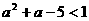 ……………10分 解得-3<a<2…………12分
……………10分 解得-3<a<2…………12分
18.(12分)证明:(1)∵四边形AA1C1C是菱形,∠C1CA=60°,∴△AC1A1是正三角形,又P是A1C1
的中点,∴PA⊥A1C1,……2分 ∴PA⊥AC. 又PA⊥BC,AC∩BC=C ∴PA⊥平面ABC.……4分
(2)由(1),PA⊥平面ABC,∴PA⊥平面 A1B1C1,由△AC1A1是正三角形,∴PB1⊥A1C1, 6分
∴B1P⊥平面AA1C1C,∴B1P⊥CC1. ∴CC1与B1P所成的角的正弦值为1.…………8分
(3)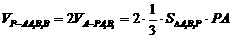 ……10分
……10分 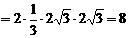 ……………12分
……………12分
17.(12分)解
(1)∵b是方程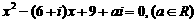 的实根,∴(b2-6b+9)+(a-b)i=02分
的实根,∴(b2-6b+9)+(a-b)i=02分
故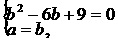 …………………4分 解得a=b=3……………………6分
…………………4分 解得a=b=3……………………6分
(2)设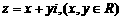 由
由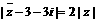 ,得
,得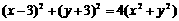 …8分
…8分
 即
即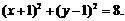 ∴z点的轨迹是以O1(-1,1)为圆心,
∴z点的轨迹是以O1(-1,1)为圆心,
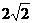 为半径的圆.……………………………10分
为半径的圆.……………………………10分
如图,当z点在OO1的连线上时,|z|有最大值或最小值,
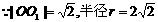 ,∴当z=1-i,时………………11分
,∴当z=1-i,时………………11分
最小值,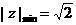 ……………………………12分
……………………………12分
13.720 14.
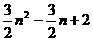 15.2; 16.
15.2; 16.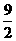
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com