
题目列表(包括答案和解析)
1.(福建卷)不等式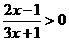 的解集是 (
A )
的解集是 (
A )
A.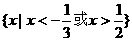 B.
B.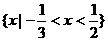
C.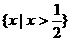 D.
D.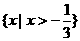
25. (江西卷)
已知数列
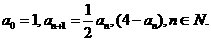
(1)证明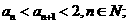
(2)求数列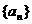 的通项公式an.
的通项公式an.
解:(1)方法一 用数学归纳法证明:
1°当n=1时,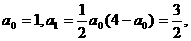
∴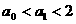 ,命题正确.
,命题正确.
2°假设n=k时有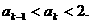
则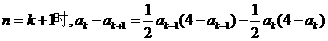
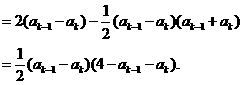
而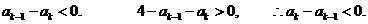
又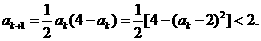
∴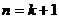 时命题正确.
时命题正确.
由1°、2°知,对一切n∈N时有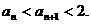
方法二:用数学归纳法证明:
1°当n=1时,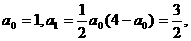 ∴
∴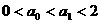 ;
;
2°假设n=k时有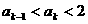 成立,
成立,
令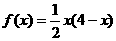 ,
,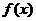 在[0,2]上单调递增,所以由假设
在[0,2]上单调递增,所以由假设
有: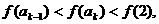 即
即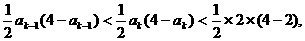
也即当n=k+1时 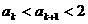 成立,所以对一切
成立,所以对一切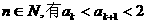
(2)下面来求数列的通项: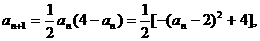 所以
所以
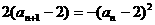
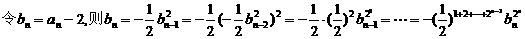 ,
,
又bn=-1,所以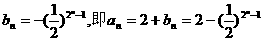
24. (江西卷)已知数列{an}的前n项和Sn满足Sn-Sn-2=3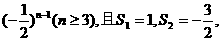 求数列{an}的通项公式.
求数列{an}的通项公式.
解:方法一:先考虑偶数项有: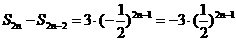
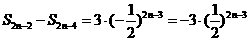
………
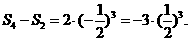
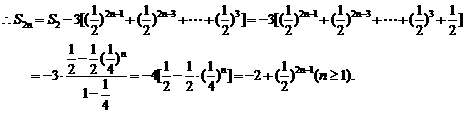
同理考虑奇数项有: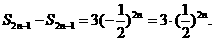
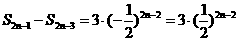
………
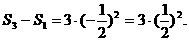
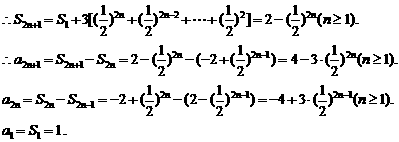
综合可得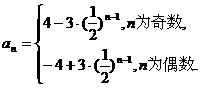
方法二:因为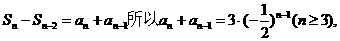
两边同乘以 ,可得:
,可得:
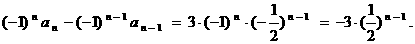
令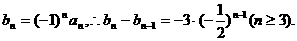
所以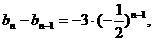
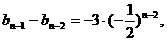
………
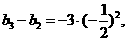
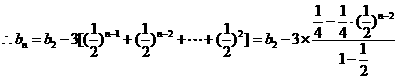
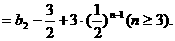
又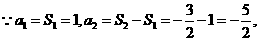
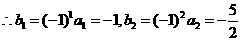
∴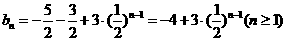
∴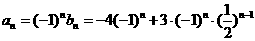
23. (重庆卷)数列{an}满足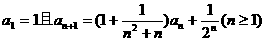 .
.
(Ⅰ)用数学归纳法证明: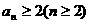 ;
;
(Ⅱ)已知不等式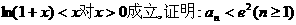 ,其中无理数e=2.71828….
,其中无理数e=2.71828….
(Ⅰ)证明:(1)当n=2时,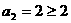 ,不等式成立.
,不等式成立.
(2)假设当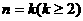 时不等式成立,即
时不等式成立,即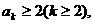
那么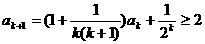 . 这就是说,当
. 这就是说,当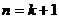 时不等式成立.
时不等式成立.
根据(1)、(2)可知: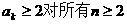 成立.
成立.
(Ⅱ)证法一:
由递推公式及(Ⅰ)的结论有
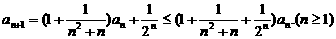
两边取对数并利用已知不等式得
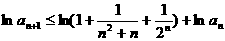
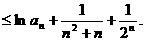 故
故
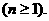
上式从1到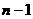 求和可得
求和可得
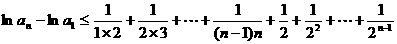
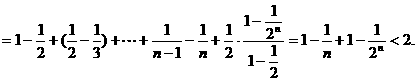
即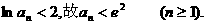
(Ⅱ)证法二:
由数学归纳法易证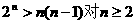 成立,故
成立,故
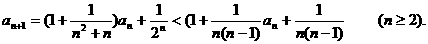
令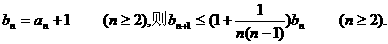
取对数并利用已知不等式得 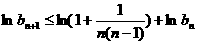
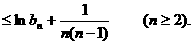
上式从2到n求和得 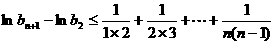
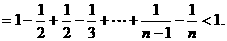
因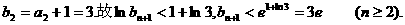
故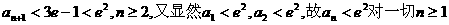 成立
成立
22. (重庆卷)数列{an}满足a1=1且8an+1-16an+1+2an+5=0
(n³1)。记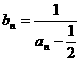 (n³1)。
(n³1)。
(1) 求b1、b2、b3、b4的值;
(2) 求数列{bn}的通项公式及数列{anbn}的前n项和Sn。
解法一:
(I)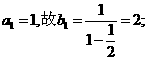
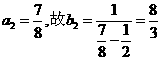
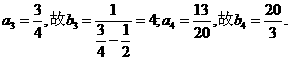
(II)因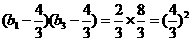 ,
,
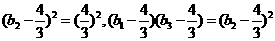
故猜想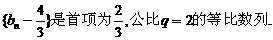
因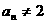 ,(否则将
,(否则将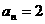 代入递推公式会导致矛盾)。
代入递推公式会导致矛盾)。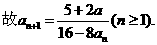
∵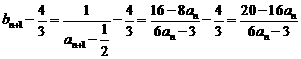
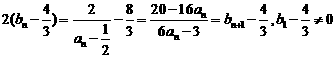
故 的等比数列.
的等比数列.
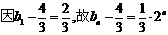 ,
, 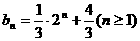
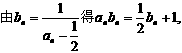
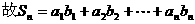
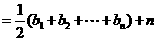
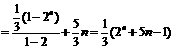
解法二:
(Ⅰ)由
整理得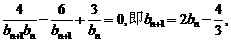
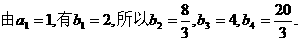
(Ⅱ)由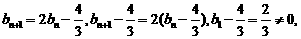
所以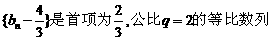
故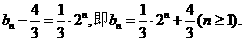
由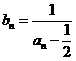 得
得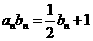
故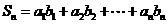
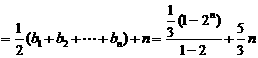
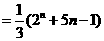
解法三:
(Ⅰ)同解法一
(Ⅱ)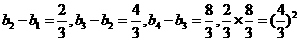
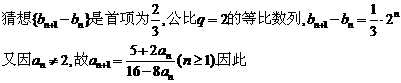
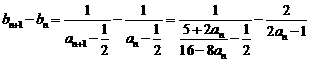
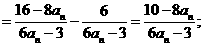
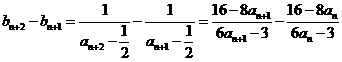
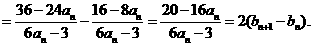
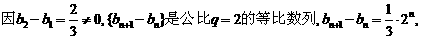
从而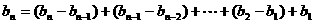
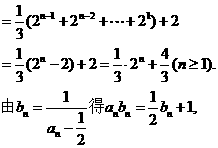
故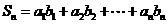
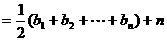
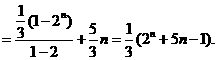
20. (浙江卷)已知实数a,b,c成等差数列,a+1,了+1,c+4成等比数列,求a,b,c.
解:由题意,得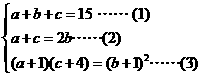 由(1)(2)两式,解得
由(1)(2)两式,解得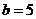
将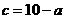 代入(3),整理得
代入(3),整理得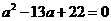
解得 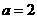 或
或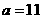
故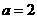 ,
,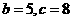 或
或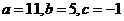
经验算,上述两组数符合题意。
21(浙江卷)设点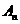 (
(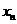 ,0),
,0),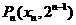 和抛物线
和抛物线 :y=x2+an x+bn(n∈N*),其中an=-2-4n-
:y=x2+an x+bn(n∈N*),其中an=-2-4n-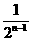 ,
,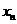 由以下方法得到:
由以下方法得到:
x1=1,点P2(x2,2)在抛物线C1:y=x2+a1x+b1上,点A1(x1,0)到P2的距离是A1到C1上点的最短距离,…,点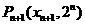 在抛物线
在抛物线 :y=x2+an x+bn上,点
:y=x2+an x+bn上,点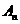 (
(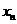 ,0)到
,0)到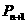 的距离是
的距离是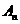 到
到 上点的最短距离.
上点的最短距离.
(Ⅰ)求x2及C1的方程.
(Ⅱ)证明{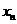 }是等差数列.
}是等差数列.
解:(I)由题意,得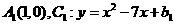 。
。
设点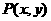 是
是 上任意一点,则
上任意一点,则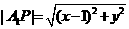
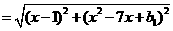
令 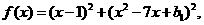 则
则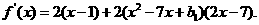
由题意,得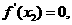 即
即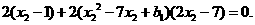
又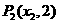 在
在 上,
上,
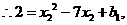
解得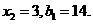
故 方程为
方程为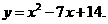
(II)设点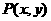 是
是 上任意一点,则
上任意一点,则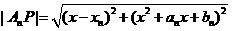
令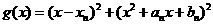 ,则
,则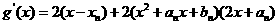 .
.
由题意得g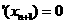 ,即
,即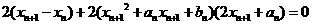
又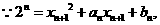
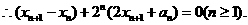 即
即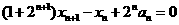 (*)
(*)
下面用数学归纳法证明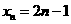
①当n=1时,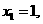 等式成立。
等式成立。
②假设当n=k时,等式成立,即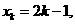
则当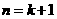 时,由(*)知
时,由(*)知 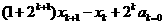
又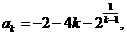
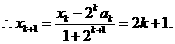
即当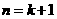 时,等式成立。
时,等式成立。
由①②知,等式对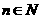 成立。
成立。
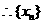 是等差数列。
是等差数列。
19. (天津卷)若公比为c的等比数列{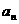 }的首项
}的首项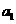 =1且满足:
=1且满足: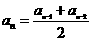 (
(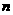 =3,4,…)。
=3,4,…)。
(I)求c的值。
(II)求数列{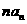 }的前
}的前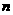 项和
项和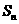 。
。
18. (天津卷)
已知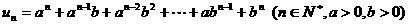 .
.
(Ⅰ)当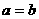 时,求数列
时,求数列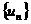 的前n项和
的前n项和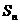 ;
;
(Ⅱ)求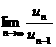 .
.
(18)解:(Ⅰ)当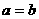 时,
时,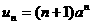 .这时数列
.这时数列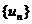 的前
的前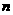 项和
项和
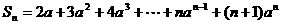 . ①
. ①
①式两边同乘以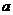 ,得
,得 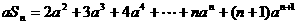 ②
②
①式减去②式,得 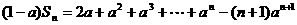
若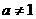 ,
,
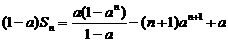 ,
,
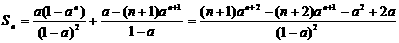
若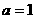 ,
,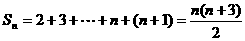
(Ⅱ)由(Ⅰ),当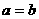 时,
时,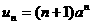 ,则
,则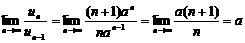 .
.
当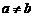 时,
时,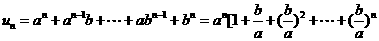
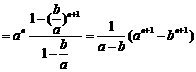
此时,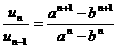 .
.
若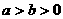 ,
,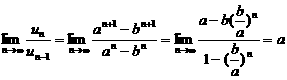 .
.
若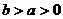 ,
,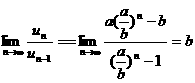 .
.
17.(上海)本题共有2个小题,第1小题满分6分, 第2小题满分8分.
假设某市2004年新建住房400万平方米,其中有250万平方米是中低价房.预计在今后的若干年内,该市每年新建住房面积平均比上一年增长8%.另外,每年新建住房中,中低价房的面积均比上一年增加50万平方米.那么,到哪一年底,
(1)该市历年所建中低价房的累计面积(以2004年为累计的第一年)将首次不少于4750万平方米?
(2)当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%?
[解](1)设中低价房面积形成数列{an},由题意可知{an}是等差数列,
其中a1=250,d=50,则Sn=250n+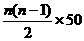 =25n2+225n,
=25n2+225n,
令25n2+225n≥4750,即n2+9n-190≥0,而n是正整数, ∴n≥10.
到2013年底,该市历年所建中低价房的累计面积将首次不少于4750万平方米.
(2)设新建住房面积形成数列{bn},由题意可知{bn}是等比数列,
其中b1=400,q=1.08,则bn=400·(1.08)n-1·0.85.
由题意可知an>0.85 bn,有250+(n-1)·50>400·(1.08)n-1·0.85.
由计箅器解得满足上述不等式的最小正整数n=6.
到2009年底,当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%.
16. (山东卷)
已知数列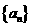 的首项
的首项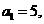 前
前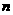 项和为
项和为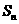 ,且
,且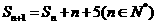
(I)证明数列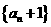 是等比数列;
是等比数列;
(II)令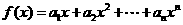 ,求函数
,求函数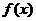 在点
在点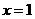 处的导数
处的导数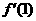 并比较
并比较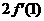 与
与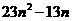 的大小.
的大小.
解:由已知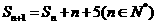 可得
可得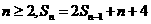 两式相减得
两式相减得
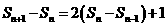 即
即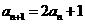 从而
从而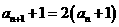 当
当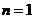 时
时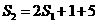 所以
所以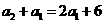 又
又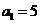 所以
所以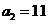 从而
从而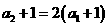
故总有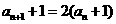 ,
,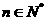 又
又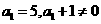 从而
从而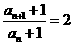 即数列
即数列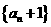 是等比数列;
是等比数列;
(II)由(I)知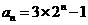
因为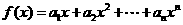 所以
所以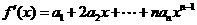
从而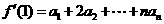 =
=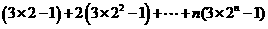
=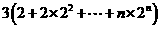 -
-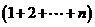 =
=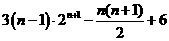
由上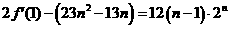 -
-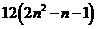 =
=
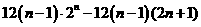 =12
=12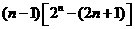 ①
①
当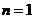 时,①式=0所以
时,①式=0所以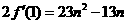 ;
;
当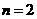 时,①式=-12
时,①式=-12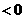 所以
所以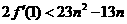
当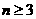 时,
时,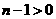 又
又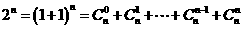

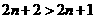
所以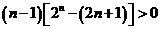 即①
即① 从而
从而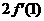

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com