
题目列表(包括答案和解析)
2.(江苏卷)设a、b、c是互不相等的正数,则下列等式中不恒成立的是
(A)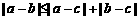 (B)
(B)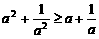
(C)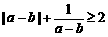 (D)
(D)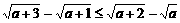
[思路点拨]本题主要考查.不等式恒成立的条件,由于给出的是不完全提干,必须结合选择支,才能得出正确的结论。
[正确解答]运用排除法,C选项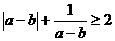 ,当a-b<0时不成立。
,当a-b<0时不成立。
[解后反思]运用公式一定要注意公式成立的条件
如果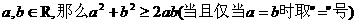
如果a,b是正数,那么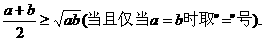
1.(安徽卷)不等式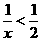 的解集是( )
的解集是( )
A.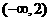 B.
B.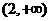 C.
C.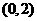 D.
D.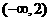
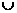
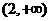
解:由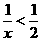 得:
得: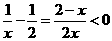 ,即
,即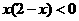 ,故选D。
,故选D。
22.设函数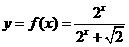 上两点P1
上两点P1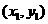 ,P2
,P2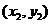 ,若
,若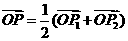 ,且P点的横坐标为
,且P点的横坐标为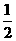 ,
,
(1)求证:P点的纵坐标为定值1;
(2)求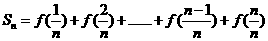
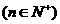
(3)记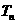 为数列
为数列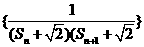 的前n项和,若
的前n项和,若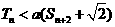 对一切
对一切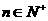 都成立,求实数a的取值范围。
都成立,求实数a的取值范围。
21.(理)己知函数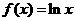 ,
,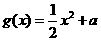 (
(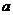 为常数),直线
为常数),直线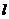 与函数
与函数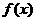 及
及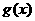 的图象都相切,且
的图象都相切,且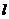 与
与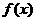 的切点的横坐标为1,
的切点的横坐标为1,
(1)求直线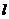 的方程及a的值;
的方程及a的值;
(2)当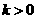 时,讨论方程
时,讨论方程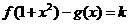 的解的个数。
的解的个数。
(文)己知函数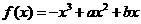 在区间(-2,1)内,当
在区间(-2,1)内,当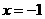 时,取得极小值,
时,取得极小值,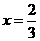 时,取得极大值,
时,取得极大值,
求(1)函数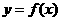 在
在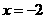 时的对应点的切线方程;
时的对应点的切线方程;
(2)函数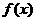 在
在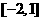 上的最大值与最小值。
上的最大值与最小值。
20.双曲线的中心是原点O,它的虚轴长为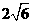 ,相应于焦点F
,相应于焦点F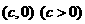 的准线
的准线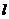 与x轴交于点A,且
与x轴交于点A,且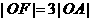 ,过点F的直线与双曲线交于P,Q两点,
,过点F的直线与双曲线交于P,Q两点,
(1)求双曲线方程及离心率;
(2)若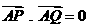 ,求直线PQ的方程。
,求直线PQ的方程。
19.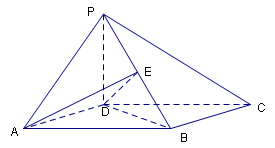 己知ABCD为矩形,PD
己知ABCD为矩形,PD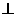 平面ABCD,PD=DC=
平面ABCD,PD=DC=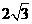 ,AD=2,E为PB上一点,且PC
,AD=2,E为PB上一点,且PC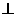 平面ADE,
平面ADE,
(1)求PC与平面PBD所成角的大小;
(2)求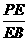 的值
的值
(3)求四棱锥P-ABCD夹在平面ADE与底面ABCD之间部分的体积。
18.(文)有一批食品出厂前要进行五项指标抽检,如果有两项指标不合格,则这批产品不能出厂,己知每项抽检是相互独立的,且每项抽检不合格的概率都是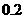 ,
,
(1)求这批食品不能出厂的概率;(保留三位有效数字)
(2)求直到五项指标全部检验完毕,才能确定该食品是否可以出厂的概率。
(理)袋中有红球3个,蓝球2个,黄球1个,任取一球确认颜色后放回袋中,最多可以取3次,但是若取到红球就不能再取了,
(1)求取出一次或二次的概率;
(2)假定每取一次可以得100元,求所得金额的期望;
(3)求恰好两次取到蓝球的概率。
17.己知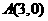 ,
,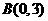 ,
,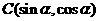 ,其中
,其中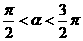 ,
,
(1)若 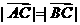 ,求
,求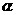 的值
的值
(2)若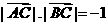 ,求
,求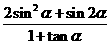 的值
的值
16.把49个数排成如图所示的数表,若表中每行7个数自左至右依次成等差数列,每列自上而下依次也成等差数列,且正中间的数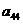 =1,则表中所有数的和为
=1,则表中所有数的和为
15.关于x的方程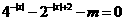 有实根,则实数m的取值范围是
有实根,则实数m的取值范围是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com