
题目列表(包括答案和解析)
19.解:(1)显然,f(x)不恒等于0,令x=1,y=0时,得f(0)=1;
(2)令y=-x≥0则1=f(x-x)=f(x)·f(-x),即f(-x)=.
由题0<f(-x)<1 ∴f(x)>1;
(3)设x1<x2,则x2-x1>0,由题得(2)知f(x)>0.
 ∴f(x2)-f(x1)=f[(x2-x1)+x1]-f(x1)=f(x2-x1)·f(x1)-f(x1)
∴f(x2)-f(x1)=f[(x2-x1)+x1]-f(x1)=f(x2-x1)·f(x1)-f(x1)
=f(x1)[f(x2-x1)-1]<0 ∴f(x2)<f(x1).
∴f(x)在R上单调递减;
(4)由已知及(3)得:M={y|y≤a},N={y|y=ax2+x+1,x∈R}
显然,当a≤0时,M∩N≠φ
当a>0时,N={y|y=a(x+)2+1-,x∈R}
要使M∩N≠φ,必须1-≤a.
即4a2-4a+1≥0 a∈R
a∈R
故所求的a的取值范围是a∈R.
18. (1)函数定义域为 ,
,
由 得
得 由
由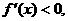 得
得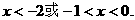
则递增区间是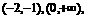 递减区间是
递减区间是 (2)由
(2)由 得
得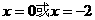 .
.
由(1)知, 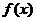 在
在 上递减,在
上递减,在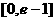 上递增.又
上递增.又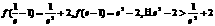 .
.
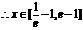 时,
时, 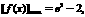 故
故 时,不等式
时,不等式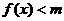 恒成立.
恒成立.
(3)方程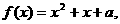 即
即 .记
.记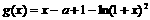 ,
,
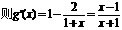 .由
.由 得
得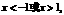 由
由 得
得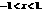
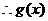 在
在 上递减,
上递减,
在 上递增. 为使
上递增. 为使 在
在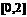 上恰好有两个相异的实根,只须
上恰好有两个相异的实根,只须
在 和
和 上各有一个实根,于是{
上各有一个实根,于是{ 解得
解得
17.解:⑴由题意知: ,
,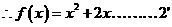
设函数 图象上的任意一点
图象上的任意一点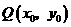 关于原点的对称点为P(x,y),则
关于原点的对称点为P(x,y),则
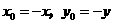 ,因为点
,因为点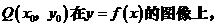
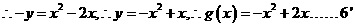
⑵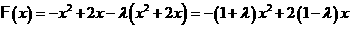
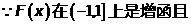 连续,
连续,
即 ,由
,由 上为减函数,当
上为减函数,当
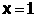 时取最小值0,故
时取最小值0,故
另解: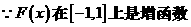 ,
,
 ,解得
,解得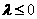
22.定义函数 ,
,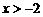 ,
, ,其导函数记为
,其导函数记为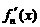 。
。
(Ⅰ)求证: ;(Ⅱ)设
;(Ⅱ)设 ,求证:
,求证: ;
;
(Ⅲ)是否存在区间 ,使函数
,使函数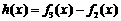 在区间
在区间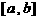 上的值
上的值
域为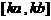 ?若存在,求出最小的
?若存在,求出最小的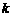 值及相应的区间
值及相应的区间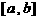 ;若不存在,请说明理由。
;若不存在,请说明理由。
DCCDA DADCD CA ②③④ 26 9 ①②
21.(本题满分12分)
已知函数f(x)在(-1,1)上有定义,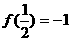 且满足x、y∈(-1,1) 有
且满足x、y∈(-1,1) 有
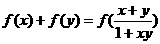 .
.
(Ⅰ)证明:f(x)在(-1,1)上为奇函数;
(Ⅱ)对数列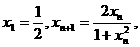 求
求 ;
;
(Ⅲ)(理)求证
20.(本小题满分12分
已知二次函数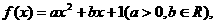 设方程f(x)=x有两个实数根x1、x2.
设方程f(x)=x有两个实数根x1、x2.
(Ⅰ)如果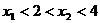 ,设函数f(x)的对称轴为x=x0,求证x0>-1;
,设函数f(x)的对称轴为x=x0,求证x0>-1;
(Ⅱ)如果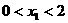 ,且f(x)=x的两实根相差为2,求实数b
的取值范围.
,且f(x)=x的两实根相差为2,求实数b
的取值范围.
19.设函数f(x)的定义域为R,对于任意实数x,y,总有f(x+y)=f(x)f(y),且当x>0时,0<f(x)<1.
(1)求f(0)的值;(2)证明:当x<0时,f(x)>1;
(3)证明:f(x)在R上单调递减;(4)若M={y|f(y)·f(1-a)≥f(1)},N={y|f(ax2+x+1-y)=1,x∈R},且M∩N≠φ,求a的取值范围.
18.设函数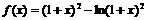 (1)求函数
(1)求函数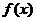 的单调区间;(2)当
的单调区间;(2)当 时,不等式
时,不等式 恒成立,求实数m的取值范围;(3)关于x的方程
恒成立,求实数m的取值范围;(3)关于x的方程 上恰有两个相异实根,求a的取值范围.
上恰有两个相异实根,求a的取值范围.
17、已知函数 的图像过点
的图像过点 ,且
,且 对任意实数都成立,函数
对任意实数都成立,函数 与
与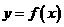 的图像关于原点对称。
的图像关于原点对称。
⑴ 求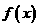 与
与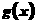 的解析式;
的解析式;
⑵ 若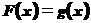 -
- 在[-1,1]上是增函数,求实数λ的取值范围;
在[-1,1]上是增函数,求实数λ的取值范围;
16.设函数f(x)=x|x|+bx+c,给出下列命题:
①b=0, c>0 时,方程f(x)=0只有一个实数根;②c=0时,y=f(x)是奇函数;
③方程f(x)=0至多有两个实根.
上述四个命题中所有的正确命题的序号为 .
兰山区高考补习学校05-06学年下学期函数与导数测试题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com