
题目列表(包括答案和解析)
9.已知lg3,lg(sinx-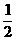 ),lg(1-y)顺次成等差数列,则
),lg(1-y)顺次成等差数列,则
A.y有最小值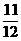 ,无最大值 B.y有最大值1,无最小值
,无最大值 B.y有最大值1,无最小值
C.y有最小值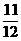 ,最大值1 D.y有最小值-1,最大值1
,最大值1 D.y有最小值-1,最大值1
8.已知y=loga(2-ax)在[0,1]上是x的减函数,则a的取值范围是
A.(0,1) B.(1,2)
C.(0,2) D.[2,+∞
7.曲线y=x3在点P处的切线斜率为k,当k=3时的P点坐标为
A.(-2,-8) B.(-1,-1),(1,1)
C.(2,8) D.(-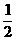 ,-
,-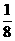 )
)
6.在100个零件中,有一级品20个,二级品30个,三级品50个,从中抽取20个作为样本:①采用随机抽样法,将零件编号为00,01,02,…,99,抽出20个;②采用系统抽样法,将所有零件分成20组,每组5个,然后每组中随机抽取1个;③采用分层抽样法,随机从一级品中抽取4个,二级品中抽取6个,三级品中抽取10个;则
A.不论采取哪种抽样方法,这100个零件中每个被抽到的概率都是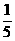
B.①②两种抽样方法,这100个零件中每个被抽到的概率都是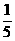 ,③并非如此
,③并非如此
C.①③两种抽样方法,这100个零件中每个被抽到的概率都是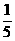 ,②并非如此
,②并非如此
D.采用不同的抽样方法,这100个零件中每个被抽到的概率各不相同
5.已知直线m,n和平面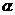 ,那么m∥n的一个必要但非充分条件是
,那么m∥n的一个必要但非充分条件是
A.m∥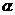 ,n∥
,n∥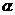 B.m⊥
B.m⊥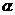 ,n⊥
,n⊥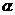
C.m∥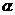 且n
且n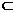
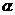 D.m,n与
D.m,n与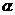 成等角
成等角
4.函数y=1-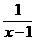 , 则下列说法正确的是
, 则下列说法正确的是
A.y在(-1,+∞)内单调递增 B.y在(-1,+∞)内单调递减
C.y在(1,+∞)内单调递增 D.y在(1,+∞)内单调递减
3.过原点的直线与圆x2+y2+4x+3=0相切,若切点在第三象限,则该直线的方程是
A.y=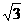 x B.y=-
x B.y=-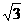 x
x
C.y= x D.y=-
x D.y=- x
x
2.已知f(x)=sin(x+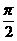 ,g(x)=cos(x-
,g(x)=cos(x-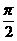 ),则f(x)的图象
),则f(x)的图象
A.与g(x)的图象相同
B.与g(x)的图象关于y轴对称
C.向左平移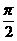 个单位,得到g(x)的图象
个单位,得到g(x)的图象
D.向右平移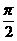 个单位,得到g(x)的图象
个单位,得到g(x)的图象
1.集合A={x|x=2k,k∈Z},B={x|x=2k+1,k∈Z},C={x|x=4k+1,k∈Z},又a∈A,b∈B,则有
A.a+b∈A
B.a+b∈B
C.a+b∈C
D.a+b不属于A,B,C中的任意一个
17三角形ABC的三个内角A、B、C,求当A满足何值时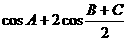 取得最大值,并求出这个最大值
取得最大值,并求出这个最大值
18)(本题满分12分)
A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验。每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效。若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组。设每只小白鼠服用A有效的概率为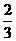 ,服用B有效的概率为
,服用B有效的概率为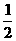 .
.
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ)观察3个试验组,用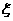 表示这3个试验组中甲类组的个数,求
表示这3个试验组中甲类组的个数,求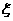 的分布列和数学期望。
的分布列和数学期望。
(19)(本题满分12分)
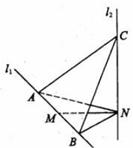 如图,
如图,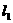 、
、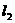 是互相垂直的异面直线,MN是它们的公垂线段。点A、B在
是互相垂直的异面直线,MN是它们的公垂线段。点A、B在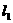 上,C在
上,C在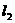 上,AM=MB=MN。
上,AM=MB=MN。
(Ⅰ)证明AC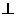 NB
NB
(Ⅱ)若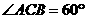 ,求NB与平面ABC所成角的余弦值.
,求NB与平面ABC所成角的余弦值.
20(12分)在平面直角坐标系xoy中,有一个点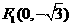 和
和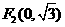 为焦点,离心率为
为焦点,离心率为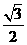 的椭圆,设椭圆在第一象限的部分曲线为C,动点P在C上,C在P点处的切线与x、y轴的交点分别为A、B,且向量
的椭圆,设椭圆在第一象限的部分曲线为C,动点P在C上,C在P点处的切线与x、y轴的交点分别为A、B,且向量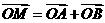 ,求
,求
(1) 点M的轨迹方程;
(2)
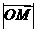 的最小值
的最小值
(21)(本小题满分14分)已知函数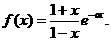
(Ⅰ)设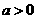 ,讨论
,讨论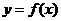 的单调性;
的单调性;
(Ⅱ)若对任意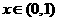 恒有
恒有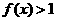 ,求
,求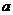 的取值范围。
的取值范围。
(22)(本小题满分12分)
设数列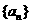 的前
的前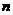 项和
项和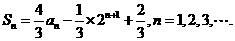
(Ⅰ)求首项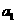 与通项
与通项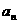 ;
;
(Ⅱ)设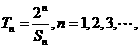 证明:
证明: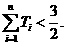
数学理科试题第1页(共4页)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com