
题目列表(包括答案和解析)
9、已知函数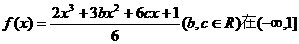 单调递增,在[1,3]单调递减. (1)求b、c之间的关系式;
单调递增,在[1,3]单调递减. (1)求b、c之间的关系式;
(2)当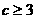 时,是否存在实数m,使得
时,是否存在实数m,使得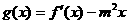 在区间
在区间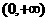 上是单调函数?若存在,求出m的取值范围,若不存在,请说明理由.
上是单调函数?若存在,求出m的取值范围,若不存在,请说明理由.
8、已知: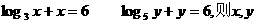 的大小关系是
.
的大小关系是
.
7、已知双曲线的离心率为2,则它的两条渐近线所成的锐角等于 .
6、如果直线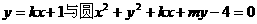 并于M、N两点,且M、N关于直
并于M、N两点,且M、N关于直
线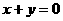 对称,则不等式组:
对称,则不等式组: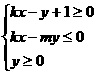 表示的平面区域的面积是 ( )
表示的平面区域的面积是 ( )
A.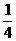 B.
B.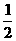 C.1 D.2
C.1 D.2
5、若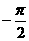 <
<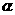 <0,则直线x·tan
<0,则直线x·tan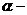 y=0的倾斜角为
(
)
y=0的倾斜角为
(
)
A.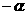 B.
B.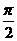 +
+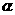 C.
C.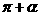 D.
D.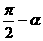
4、在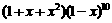 的展开式中,
的展开式中,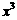 的系数是 ( )
的系数是 ( )
A.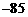 B.
B.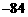 C.
C. D.
D.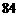
3、已知m、n为两条不同的直线α、β为两个不同的平面,给出下列四个命题
①若m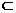 α,n//α,则m//n ; ②若m⊥α,n//α,则m⊥n;
α,n//α,则m//n ; ②若m⊥α,n//α,则m⊥n;
③若m⊥α,m⊥β,则α//β; ④若m//α,n//α,则m//n.
其中真命题的序号是 ( )
A.①② B.③④ C.①④ D.②③
2、已知f(x)是定义在R上的偶函数,且在[0,+∞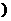 上是单调递增函数,若f(x1)> f(x2),则下列结论一定成立的是
(
)
上是单调递增函数,若f(x1)> f(x2),则下列结论一定成立的是
(
)
A.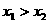 B.
B.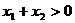 C.
C.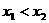 D.
D.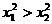
1、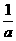 <
<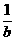 成立的一个充分不必要条件是
(
)
成立的一个充分不必要条件是
(
)
A.a>b B.a<0<b C.a<b D.ab>0
7. (全国卷Ⅰ) (13)若正整数m满足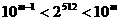 ,则m = 155
。
,则m = 155
。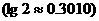
解答题:
1(湖北卷)22.(本小题满分14分)
已知不等式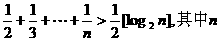 为大于2的整数,
为大于2的整数,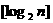 表示不超过
表示不超过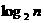 的最大整数. 设数列
的最大整数. 设数列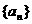 的各项为正,且满足
的各项为正,且满足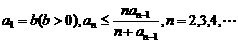
(Ⅰ)证明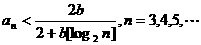
(Ⅱ)猜测数列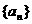 是否有极限?如果有,写出极限的值(不必证明);
是否有极限?如果有,写出极限的值(不必证明);
(Ⅲ)试确定一个正整数N,使得当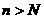 时,对任意b>0,都有
时,对任意b>0,都有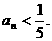
解:(Ⅰ)证法1:∵当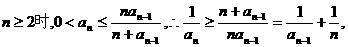
即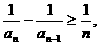
于是有 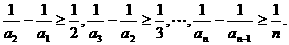
所有不等式两边相加可得 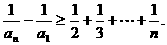
由已知不等式知,当n≥3时有,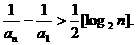
∵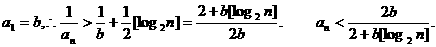
证法2:设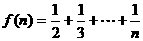 ,首先利用数学归纳法证不等式
,首先利用数学归纳法证不等式
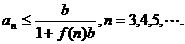
(i)当n=3时, 由 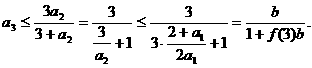
知不等式成立.
(ii)假设当n=k(k≥3)时,不等式成立,即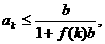
则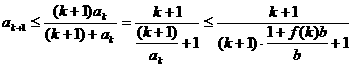
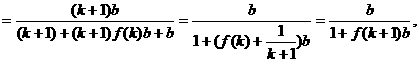
即当n=k+1时,不等式也成立.
由(i)、(ii)知,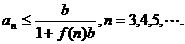
又由已知不等式得 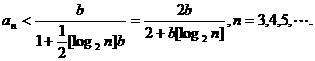
(Ⅱ)有极限,且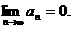
(Ⅲ)∵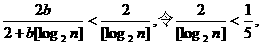
则有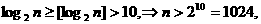
故取N=1024,可使当n>N时,都有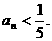
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com