
题目列表(包括答案和解析)
3.下列函数中既是奇函数,又在区间(0,+∞)上单调递增的是 ( )
A. B.
B.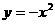 C.
C.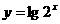 D.
D.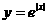
2.如果复数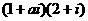 的实部和虚部相等,则实数
的实部和虚部相等,则实数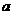 等于 ( )
等于 ( )
A.-1 B.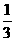 C.
C.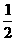 D.1
D.1
1.已知集合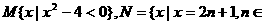 Z),则集合
Z),则集合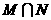 等于 ( )
等于 ( )
A.{-1,1} B.{-1,0,1} C.{0,1} D.{-1,0}
10、C(理)由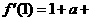
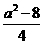 知
知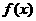 在点
在点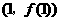 处的切线
处的切线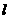 的方程是
的方程是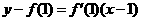 ,即
,即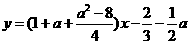 ,因为切线
,因为切线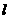 在x=1处穿过
在x=1处穿过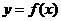 的图象,所以
的图象,所以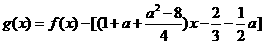 在
在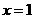 两边附近的函数值异号,则
两边附近的函数值异号,则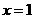 不是
不是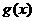 的极值点.
的极值点.
而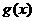
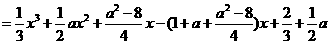 ,且
,且
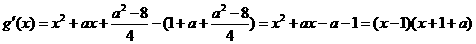 .
.
若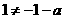 ,则
,则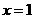 和
和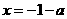 都是
都是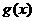 的极值点.
的极值点.
所以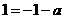 ,即
,即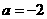 .
.
(文)当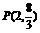 为切点时,
为切点时,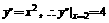 所求切线方程为
所求切线方程为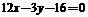 ;当
;当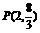 不是切点时,设切点为
不是切点时,设切点为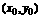 ,则
,则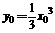 ,又切线斜率为
,又切线斜率为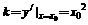 ,所以
,所以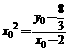 ,
,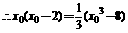 ,解得
,解得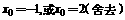 ,此时切线的斜率为1,切线方程为
,此时切线的斜率为1,切线方程为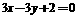 ,综上所述,所求切线为
,综上所述,所求切线为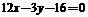 或
或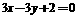 。
。
9、D(理)显然2-a2 =b2-2,即a2 +b2 =4,然后用几何法三角换元法均值不等式都可以得到。
(文)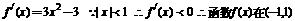 上单调递减,所以无
上单调递减,所以无
最大、最小值。
8、A由f(x)=-f(x+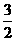 )得f(x)=f(x+3)即周期为3,由图像关于点(-
)得f(x)=f(x+3)即周期为3,由图像关于点(-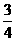 ,0)成中心对称得f(x)+f(-x-
,0)成中心对称得f(x)+f(-x-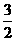 )=0,从而-f(x+
)=0,从而-f(x+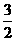 )=- f(-x-
)=- f(-x-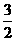 ),所以f(x)= f(-x)。f(1)=f(4)=...=f(2008)=1,由f(-1)=1,可得出f(2)=f(5)=...=f(2009)=1,由f(0)=-2,可得出f(3)=f(6)=...=f(2010)=-2
),所以f(x)= f(-x)。f(1)=f(4)=...=f(2008)=1,由f(-1)=1,可得出f(2)=f(5)=...=f(2009)=1,由f(0)=-2,可得出f(3)=f(6)=...=f(2010)=-2
7、C(理)令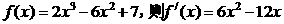 =
=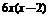
由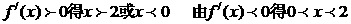 ,
,
又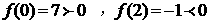
(文)零点定理的逆定理不一定为真
6、C函数 f(x-1)是由f(x)向右平移一个单位得到,f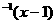 由f
由f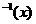 向右平移一个单位得到,而f(x)和f
向右平移一个单位得到,而f(x)和f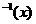 关于y=x对称,从而f(x-1)与f
关于y=x对称,从而f(x-1)与f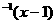 的对称轴也是由原对称轴向右平移一个单位得到即y=x-1
的对称轴也是由原对称轴向右平移一个单位得到即y=x-1
5、D由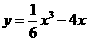 得
得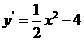 ,切线的倾斜角小于
,切线的倾斜角小于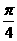 ,则
,则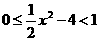 ,所以
,所以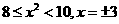 ,即点
,即点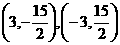 两点的切线倾斜角小于
两点的切线倾斜角小于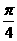 .
.
4、C(理)曲线在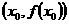 处有导数,则切线一定存在,但有切线,切线的斜率可能不存在,即导数不存在.
处有导数,则切线一定存在,但有切线,切线的斜率可能不存在,即导数不存在.
(文)该题一般都认为是选A,依照教科书上的结论:“一般地,设函数y=f(x)在某个区间内有导数,如果在这个区间内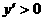 ,那么y=f(x)为这个区间内的增函数;如果在这个区间内
,那么y=f(x)为这个区间内的增函数;如果在这个区间内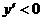 ,那么y=f(x)为这个区间内的减函数。”致错的原因是没有准确理解上述这段话的逻辑关系,事实上这是一个充分非必要条件。例如,函数f(x)=x3在(-∞,+∞)是单调递增的,然而却有
,那么y=f(x)为这个区间内的减函数。”致错的原因是没有准确理解上述这段话的逻辑关系,事实上这是一个充分非必要条件。例如,函数f(x)=x3在(-∞,+∞)是单调递增的,然而却有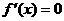 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com