
题目列表(包括答案和解析)
3.圆锥轴截面两腰的夹角叫圆锥的顶角.
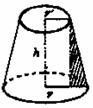
①如图,圆锥的顶角为β,母线与下底面所成角为α,母线为l,高为h,底面半径为r,则
 sinα=cos
sinα=cos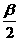 =
=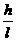 ,
,
α+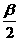 =90°
=90°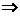
cosα=sin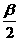 =
=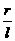 .
.
②圆台 如图,圆台母线与下底面所成角为α,母线为l,高为h,上、下底面半径分别为r ′、r,则h=lsinα,r-r′=lcosα。
③球的截面
用一个平面去截一个球,截面是圆面.
(1)过球心的截面截得的圆叫做球的大圆;不经过球心的截面截得的圆叫做球的小圆;
(2)球心与截面圆圆心的连线垂直于截面;
(3)球心和截面距离d,球半径R,截面半径r有关系:
r=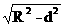 .
.
2.直角四面体的性质 有一个三面角的各个面角都是直角的四面体叫做直角四面体.直角四面 体有下列性质:
如图,在直角四面体AOCB中,∠AOB=∠BOC=∠COA=90°,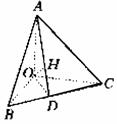 OA=a,OB=b,OC=c。
OA=a,OB=b,OC=c。
则:①不含直角的底面ABC是锐角三角形;
②直角顶点O在底面上的射影H是△ABC的垂心;
③体积 V=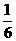 abc;
abc;
④底面△ABC=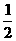
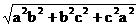 ;
;
⑤S2△ABC=S△BHC·S△ABC;
⑥S2△BOC=S2△AOB+S2△AOC=S2△ABC
⑦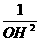 =
=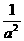 +
+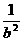 +
+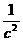 ;
;
⑧外切球半径 R=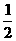
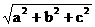 ;
;
⑨内切球半径 r=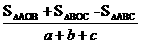
1.正四面体的性质 设正四面体的棱长为a,则这个正四面体的
(1)全面积:S全=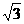 a2;
a2;
(2)体积:V=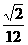 a3;
a3;
(3)对棱中点连线段的长:d=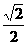 a;
a;
(4)内切球半径:r=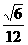 a;
a;
(5)外接球半径 R=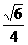 a;
a;
(6)正四面体内任意一点到四个面的距离之和为定值(等于正四面体的高)。
即l2=16
所以l=4(cm)。
点评:涉及棱柱面积问题的题目多以直棱柱为主,而直棱柱中又以正方体、长方体的表面积多被考察。我们平常的学习中要多建立一些重要的几何要素(对角线、内切)与面积、体积之间的关系。
例2.如图1所示,在平行六面体ABCD-A1B1C1D1中,已知AB=5,AD=4,AA1=3,AB⊥AD,∠A1AB=∠A1AD=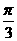 。
。
(1)求证:顶点A1在底面ABCD上的射影O在∠BAD的平分线上;
(2)求这个平行六面体的体积
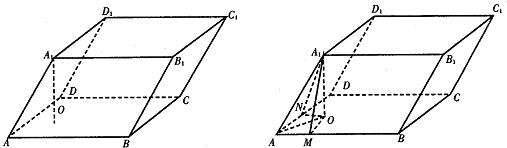
图1 图2
解析:(1)如图2,连结A1O,则A1O⊥底面ABCD。作OM⊥AB交AB于M,作ON⊥AD交AD于N,连结A1M,A1N。由三垂线定得得A1M⊥AB,A1N⊥AD。∵∠A1AM=∠A1AN,
∴Rt△A1NA≌Rt△A1MA,∴A1M=A1N,
从而OM=ON。
∴点O在∠BAD的平分线上。
(2)∵AM=AA1cos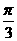 =3×
=3×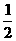 =
=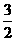
∴AO=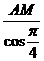 =
=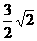 。
。
又在Rt△AOA1中,A1O2=AA12 – AO2=9-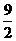 =
=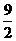 ,
,
∴A1O=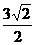 ,平行六面体的体积为
,平行六面体的体积为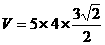
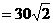 。
。
题型2:柱体的表面积、体积综合问题
例3.一个长方体共一顶点的三个面的面积分别是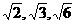 ,这个长方体对角线的长是( )
,这个长方体对角线的长是( )
A.2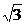 B.3
B.3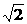 C.6 D.
C.6 D.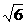
解析:设长方体共一顶点的三边长分别为a=1,b=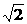 ,c=
,c=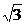 ,则对角线l的长为l=
,则对角线l的长为l=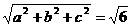 ;答案D。
;答案D。
点评:解题思路是将三个面的面积转化为解棱柱面积、体积的几何要素-棱长。
例4.如图,三棱柱ABC-A1B1C1中,若E、F分别为AB、AC 的中点,平面EB1C1将三棱柱分成体积为V1、V2的两部分,那么V1∶V2= ____ _。
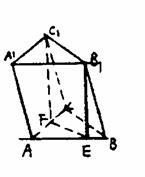 解:设三棱柱的高为h,上下底的面积为S,体积为V,则V=V1+V2=Sh。
解:设三棱柱的高为h,上下底的面积为S,体积为V,则V=V1+V2=Sh。
∵E、F分别为AB、AC的中点,
∴S△AEF=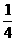 S,
S,
V1=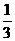 h(S+
h(S+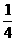 S+
S+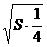 )=
)=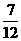 Sh
Sh
V2=Sh-V1=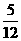 Sh,
Sh,
∴V1∶V2=7∶5。
点评:解题的关键是棱柱、棱台间的转化关系,建立起求解体积的几何元素之间的对应关系。最后用统一的量建立比值得到结论即可
题型3:锥体的体积和表面积
 例5. 7. (2009山东卷理)一空间几何体的三视图如图所示,则该几何体的体积为(
).
例5. 7. (2009山东卷理)一空间几何体的三视图如图所示,则该几何体的体积为(
).
A.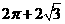 B.
B. 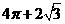 C.
C.
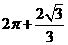 D.
D.
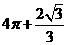
[解析]:该空间几何体为一圆柱和一四棱锥组成的,
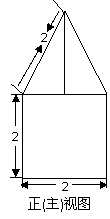
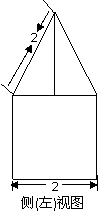 圆柱的底面半径为1,高为2,体积为
圆柱的底面半径为1,高为2,体积为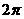 ,四棱锥的底面
,四棱锥的底面
边长为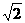 ,高为
,高为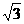 ,所以体积为
,所以体积为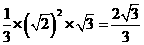
所以该几何体的体积为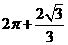 .
.
答案:C
[命题立意]:本题考查了立体几何中的空间想象能力,
由三视图能够想象得到空间的立体图,并能准确地
计算出.几何体的体积.
(2009四川卷文)如图,已知六棱锥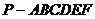 的底面是正六边形,
的底面是正六边形,
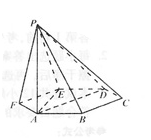
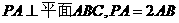 则下列结论正确的是
则下列结论正确的是
A. 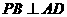
B. 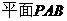
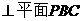
C. 直线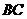 ∥
∥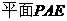
D. 直线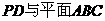 所成的角为45°
所成的角为45°
[答案]D
[解析]∵AD与PB在平面的射影AB不垂直,所以A不成立,又,平面PAB⊥平面PAE,所以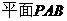
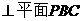 也不成立;BC∥AD∥平面PAD, ∴直线
也不成立;BC∥AD∥平面PAD, ∴直线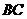 ∥
∥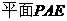 也不成立。在
也不成立。在 中,PA=AD=2AB,∴∠PDA=45°. ∴D正确
中,PA=AD=2AB,∴∠PDA=45°. ∴D正确
(2009全国卷Ⅱ文)设OA是球O的半径,M是OA的中点,过M且与OA成45°角的平面截球O的表面得到圆C。若圆C的面积等于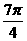 ,则球O的表面积等于 ×
,则球O的表面积等于 ×
答案:8π
解析:本题考查立体几何球面知识,注意结合平面几何知识进行运算,由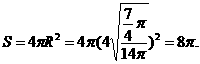
例61.(2009年广东卷文)(本小题满分13分)
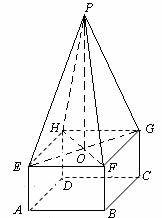
某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P-EFGH,下半部分是长方体ABCD-EFGH.图5、图6分别是该标识墩的正(主)视图和俯视图.
(1)请画出该安全标识墩的侧(左)视图;
(2)求该安全标识墩的体积
(3)证明:直线BD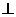 平面PEG
平面PEG
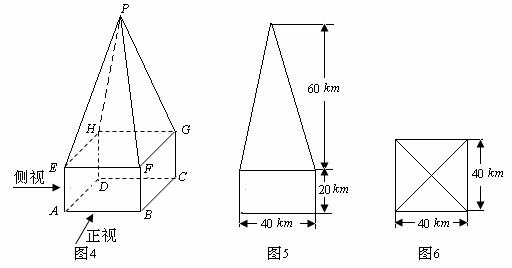
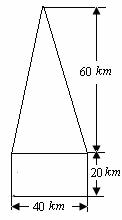 [解析](1)侧视图同正视图,如下图所示.
[解析](1)侧视图同正视图,如下图所示.
(2)该安全标识墩的体积为: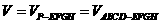
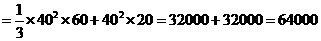
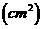
(3)如图,连结EG,HF及 BD,EG与HF相交于O,连结PO.
由正四棱锥的性质可知, 平面EFGH
,
平面EFGH
, 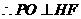
又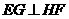
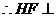 平面PEG
平面PEG
又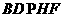
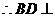 平面PEG
平面PEG
例7.ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GB垂直于正方形ABCD所在的平面,且GC=2,求点B到平面EFC的距离?
解:如图,取EF的中点O,连接GB、GO、CD、FB构造三棱锥B-EFG。
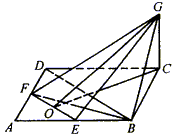
设点B到平面EFG的距离为h,BD=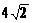 ,EF
,EF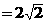 ,CO=
,CO=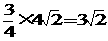 。
。
 。
。
而GC⊥平面ABCD,且GC=2。
由 ,得
,得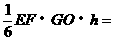
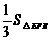 ·
·
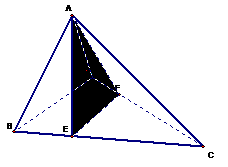 点评:该问题主要的求解思路是将点面的距离问题转化为体积问题来求解。构造以点B为顶点,△EFG为底面的三棱锥是解此题的关键,利用同一个三棱锥的体积的唯一性列方程是解这类题的方法,从而简化了运算。
点评:该问题主要的求解思路是将点面的距离问题转化为体积问题来求解。构造以点B为顶点,△EFG为底面的三棱锥是解此题的关键,利用同一个三棱锥的体积的唯一性列方程是解这类题的方法,从而简化了运算。
例8.2009年上海卷理)已知三个球的半径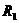 ,
,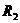 ,
,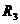 满足
满足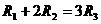 ,则它们的表面积
,则它们的表面积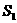 ,
,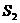 ,
,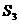 ,满足的等量关系是___________.
,满足的等量关系是___________.
[答案]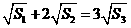
[解析]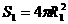 ,
,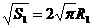 ,同理:
,同理: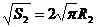
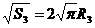 ,即R1=
,即R1=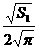 ,R2=
,R2=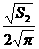 ,R3=
,R3=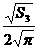 ,由
,由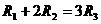 得
得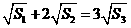
例9.(2009安徽卷文)(本小题满分13分)
如图,ABCD的边长为2的正方形,直线l与平面ABCD平行,g和F式l上的两个不同点,且EA=ED,FB=FC, 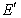 和
和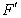 是平面ABCD内的两点,
是平面ABCD内的两点,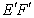 和
和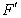
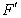 都与平面ABCD垂直,
都与平面ABCD垂直,
(Ⅰ)证明:直线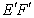 垂直且平分线段AD
垂直且平分线段AD
(Ⅱ)若∠EAD=∠EAB=60°,EF=2,求多面
体ABCDEF的体积。
[思路]根据空间线面关系可证线线垂直,由分割法可求得多面体体积,体现的是一种部分与整体的基本思想
[解析](1)由于EA=ED且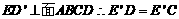
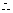 点E
点E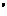 在线段AD的垂直平分线上,同理点F
在线段AD的垂直平分线上,同理点F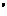 在线段BC的垂直平分线上.
在线段BC的垂直平分线上.
又ABCD是四方形
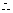 线段BC的垂直平分线也就是线段AD的垂直平分线
线段BC的垂直平分线也就是线段AD的垂直平分线
即点E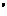 F
F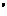 都居线段AD的垂直平分线上
都居线段AD的垂直平分线上
所以,直线E F
F 垂直平分线段AD.
垂直平分线段AD.
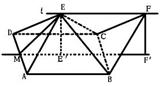 (2)连接EB、EC由题意知多面体ABCD可分割成正四棱锥E-ABCD和正四面体E-BCF两部分.设AD中点为M,在Rt△MEE
(2)连接EB、EC由题意知多面体ABCD可分割成正四棱锥E-ABCD和正四面体E-BCF两部分.设AD中点为M,在Rt△MEE 中,由于ME
中,由于ME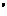 =1,
=1,
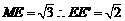 .
.
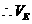 -ABCD
-ABCD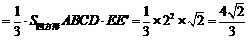
又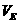 -BCF=VC-BEF=VC-BEA=VE-ABC
-BCF=VC-BEF=VC-BEA=VE-ABC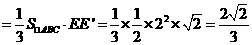
 多面体ABCDEF的体积为VE-ABCD+VE-BCF=
多面体ABCDEF的体积为VE-ABCD+VE-BCF=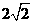
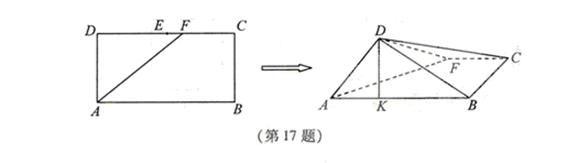
例10.(1)(2009浙江卷理)如图,在长方形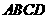 中,
中,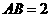 ,
,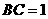 ,
,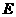 为
为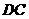 的中点,
的中点,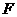 为线段
为线段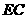 (端点除外)上一动点.现将
(端点除外)上一动点.现将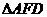 沿
沿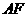 折起,使平面
折起,使平面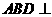 平面
平面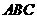 .在平面
.在平面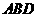 内过点
内过点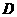
作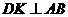 ,
,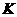 为垂足.设
为垂足.设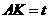 ,则
,则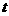 的取值范围是
.
的取值范围是
.
答案: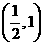
[解析]此题的破解可采用二个极端位置法,即对于F位于DC的中点时,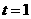 ,随着F点到C点时,因
,随着F点到C点时,因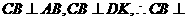 平面
平面 ,即有
,即有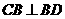 ,对于
,对于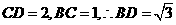 ,又
,又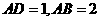 ,因此有
,因此有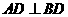 ,则有
,则有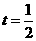 ,因此
,因此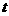 的取值范围是
的取值范围是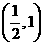
例11.3.(2009浙江卷文)若某几何体的三视图(单位: )如图所示,则此几何体的体积是
)如图所示,则此几何体的体积是
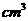 .
.
[命题意图]此题主要是考查了几何体的三视图,通过三视图的考查充分体现了几何体直观的考查要求,与表面积和体积结合的考查方法.
[解析]该几何体是由二个长方体组成,下面体积为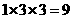 ,上面的长方体体积为
,上面的长方体体积为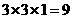 ,因此其几何体的体积为18
,因此其几何体的体积为18
例12.2009全国卷Ⅰ理)直三棱柱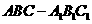 的各顶点都在同一球面上,若
的各顶点都在同一球面上,若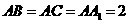 ,
,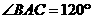 ,则此球的表面积等于 。
,则此球的表面积等于 。
解:在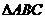 中
中 ,
,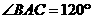 ,可得
,可得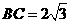 ,由正弦定理,可得
,由正弦定理,可得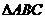 外接圆半径r=2,设此圆圆心为
外接圆半径r=2,设此圆圆心为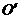 ,球心为
,球心为 ,在
,在 中,易得球半径
中,易得球半径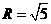 ,故此球的表面积为
,故此球的表面积为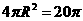 .
.
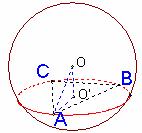 例13.已知过球面上
例13.已知过球面上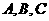 三点的截面和球心的距离为球半径的一半,且
三点的截面和球心的距离为球半径的一半,且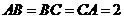 ,求球的表面积
,求球的表面积
解:设截面圆心为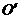 ,连结
,连结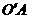 ,设球半径为
,设球半径为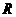 ,
,
则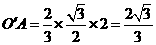 ,
,
在 中,
中,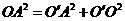 ,
,
∴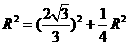 ,
,
∴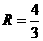 ,
,
∴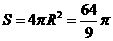 。
。
点评: 正确应用球的表面积公式,建立平面圆与球的半径之间的关系。
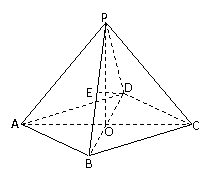
例14.如图所示,球面上有四个点P、A、B、C,如果PA,PB,PC两两互相垂直,且PA=PB=PC=a,求这个球的表面积。
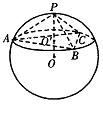
解析:如图,设过A、B、C三点的球的截面圆半径为r,圆心为O′,球心到该圆面的距离为d。
在三棱锥P-ABC中,∵PA,PB,PC两两互相垂直,且PA=PB=PC=a,
∴AB=BC=CA=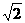 a,且P在△ABC内的射影即是△ABC的中心O′。
a,且P在△ABC内的射影即是△ABC的中心O′。
由正弦定理,得 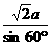 =2r,∴r=
=2r,∴r=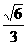 a。
a。
又根据球的截面的性质,有OO′⊥平面ABC,而PO′⊥平面ABC,
∴P、O、O′共线,球的半径R=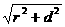 。又PO′=
。又PO′=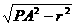 =
=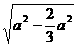 =
=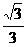 a,
a,
∴OO′=R - 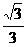 a=d=
a=d=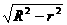 ,(R-
,(R-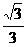 a)2=R2 – (
a)2=R2 – (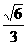 a)2,解得R=
a)2,解得R=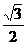 a,
a,
∴S球=4πR2=3πa2。
点评:本题也可用补形法求解。将P-ABC补成一个正方体,由对称性可知,正方体内接于球,则球的直径就是正方体的对角线,易得球半径R=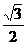 a,下略
a,下略
题型9:球的面积、体积综合问题
例15.(1)表面积为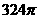 的球,其内接正四棱柱的高是
的球,其内接正四棱柱的高是 ,求这个正四棱柱的表面积。
,求这个正四棱柱的表面积。
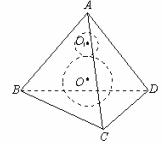
(2)正四面体ABCD的棱长为a,球O是内切球,球O1是与正四面体的三个面和球O都相切的一个小球,求球O1的体积。
解:(1)设球半径为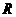 ,正四棱柱底面边长为
,正四棱柱底面边长为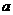 ,
,
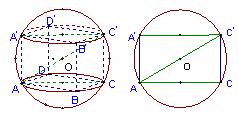
则作轴截面如图,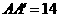 ,
,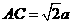 ,
,
又∵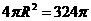 ,∴
,∴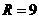 ,
,
∴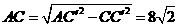 ,∴
,∴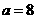 ,
,
∴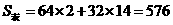
(2)如图,设球O半径为R,球O1的半径为r,E为CD中点,球O与平面ACD、BCD切于点F、G,球O1与平面ACD切于点H
由题设
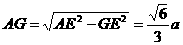
∵ △AOF∽△AEG ∴ 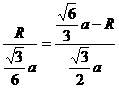 ,得
,得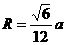
∵ △AO1H∽△AOF ∴ 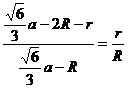 ,得
,得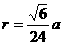
∴ 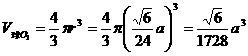
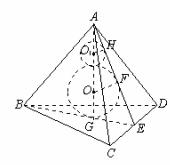
点评:正四面体的内切球与各面的切点是面的中心,球心到各面的距离相等
题型10:球的经纬度、球面距离问题
例19.(1)我国首都靠近北纬 纬线,求北纬
纬线,求北纬 纬线的长度等于多少
纬线的长度等于多少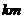 ?(地球半径大约为
?(地球半径大约为 )
)
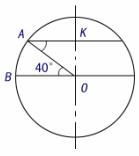 (2)在半径为
(2)在半径为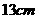 的球面上有
的球面上有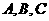 三点,
三点,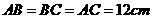 ,求球心到经过这三点的截面的距离。
,求球心到经过这三点的截面的距离。
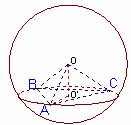
解:(1)如图, 是北纬
是北纬 上一点,
上一点,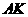 是它的半径,
是它的半径,
∴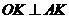 ,
,
设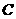 是北纬
是北纬 的纬线长,
的纬线长,
∵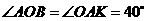 ,
,
∴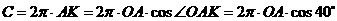
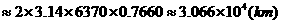
 答:北纬
答:北纬 纬线长约等于
纬线长约等于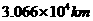 .
.
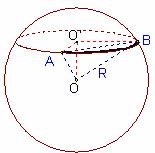
(2)解:设经过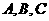 三点的截面为⊙
三点的截面为⊙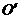 ,
,
设球心为 ,连结
,连结 ,则
,则 平面
平面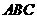 ,
,
∵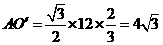 ,
,
∴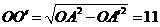 ,
,
所以,球心到截面距离为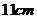 .
.
 例16.在北纬
例16.在北纬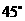 圈上有
圈上有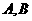 两点,设该纬度圈上
两点,设该纬度圈上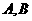 两点的劣弧长为
两点的劣弧长为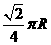 (
(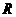 为地球半径),求
为地球半径),求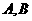 两点间的球面距离
两点间的球面距离
解:设北纬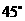 圈的半径为
圈的半径为 ,则
,则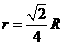 ,设
,设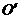 为北纬
为北纬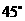 圈的圆心,
圈的圆心,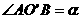 ,
,
∴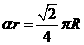 ,∴
,∴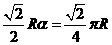 ,
,
∴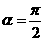 ,∴
,∴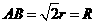 ,
,
∴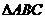 中,
中,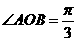 ,
,
所以,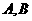 两点的球面距离等于
两点的球面距离等于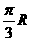 .
.
点评:要求两点的球面距离,必须先求出两点的直线距离,再求出这两点的球心角,进而求出这两点的球面距离
(2009江苏卷)(本小题满分14分)
如图,在直三棱柱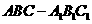 中,
中,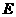 、
、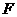 分别是
分别是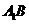 、
、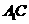 的中点,点
的中点,点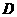 在
在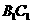 上,
上,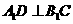 。
。
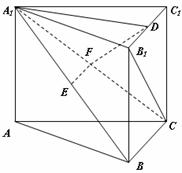 求证:(1)EF∥平面ABC;
求证:(1)EF∥平面ABC;
(2)平面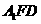
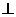 平面
平面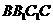 .
.
[解析] 本小题主要考查直线与平面、平面与平面得位置关系,考查空间想象能力、推理论证能力。满分14分

题型1:柱体的体积和表面积
例1.一个长方体全面积是20cm2,所有棱长的和是24cm,求长方体的对角线长.
解:设长方体的长、宽、高、对角线长分别为xcm、ycm、zcm、lcm
依题意得: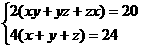
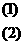
由(2)2得:x2+y2+z2+2xy+2yz+2xz=36(3)
2.旋转体的面积和体积公式
|
名称 |
圆柱 |
圆锥 |
圆台 |
球 |
|
S侧 |
2πrl |
πrl |
π(r1+r2)l |
|
|
S全 |
2πr(l+r) |
πr(l+r) |
π(r1+r2)l+π(r21+r22) |
4πR2 |
|
V |
πr2h(即πr2l) |
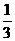 πr2h πr2h |
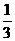 πh(r21+r1r2+r22) πh(r21+r1r2+r22) |
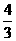 πR3 πR3 |
表中l、h分别表示母线、高,r表示圆柱、圆锥与球冠的底半径,r1、r2分别表示圆台 上、下底面半径,R表示半径
1.多面体的面积和体积公式
|
名称 |
侧面积(S侧) |
全面积(S全) |
体
积(V) |
|
|
棱 柱 |
棱柱 |
直截面周长×l |
S侧+2S底 |
S底·h=S直截面·h |
|
直棱柱 |
ch |
S底·h |
||
|
棱 锥 |
棱锥 |
各侧面积之和 |
S侧+S底 |
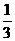 S底·h S底·h |
|
正棱锥 |
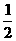 ch′ ch′ |
|||
|
棱 台 |
棱台 |
各侧面面积之和 |
S侧+S上底+S下底 |
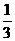 h(S上底+S下底+ h(S上底+S下底+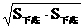 ) ) |
|
正棱台 |
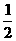 (c+c′)h′ (c+c′)h′ |
表中S表示面积,c′、c分别表示上、下底面周长,h表斜高,h′表示斜高,l表示侧棱长。
近些年来在高考中不仅有直接求多面体、旋转体的面积和体积问题,也有已知面积或体积求某些元素的量或元素间的位置关系问题。即使考查空间线面的位置关系问题,也常以几何体为依托.因而要熟练掌握多面体与旋转体的概念、性质以及它们的求积公式.同时也要学会运用等价转化思想,会把组合体求积问题转化为基本几何体的求积问题,会等体积转化求解问题,会把立体问题转化为平面问题求解,会运用“割补法”等求解。
由于本讲公式多反映在考题上,预测2010年高考有以下特色:
(1)用选择、填空题考查本章的基本性质和求积公式;
(2)考题可能为:与多面体和旋转体的面积、体积有关的计算问题;与多面体和旋转体中某些元素有关的计算问题;
了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式)。
4.注意数学中的转化思想的运用
(1)常用等角定理或平行移动直线及平面的方法转化所求角的位置;
(2)常用平行线间、平行线面间或平行平面间距离相等为依据转化所求距离的位置;
(3)常用割补法或等积(等面积或等体积)变换解决有关距离及体积问题。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com