
题目列表(包括答案和解析)
3.解:(1)证明: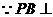 平面DEF
平面DEF
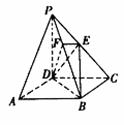
 …………1分
…………1分
又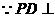 平面ABCD
平面ABCD
又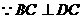
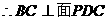 …………2分
…………2分
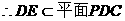
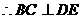
从而DE⊥平面PBC …………4分
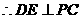 …………5分
…………5分
(2)连AC交BD于O,连EO
由PA//平面EDB
及平面EDB∩平面PAC于EO
知PA//EO …………6分
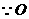 是正方形ABCD的对角线AC的中点
是正方形ABCD的对角线AC的中点
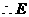 为PC的中点
为PC的中点
又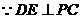
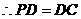
设PD=DC=a,取DC的中点H,作HG//CO交BD于G,
则HG⊥DB,EH//PD
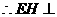 平面CDB。
平面CDB。
由三垂线定理知EG⊥BD
故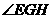 为二面角E-BD-C的一个平面角。 …………9分
为二面角E-BD-C的一个平面角。 …………9分
易求得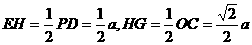
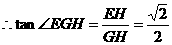
∴二面角E-BD-C的正切值为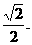 …………12分
…………12分
2.解:(1)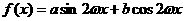
可设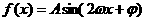 ,
,
其中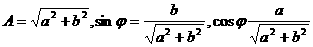
由题意知: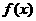 的周期为
的周期为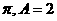
由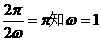
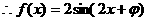 …………3分
…………3分
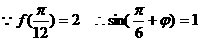
从而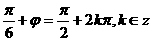
即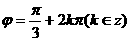
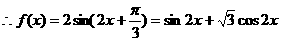
从而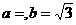 …………6分
…………6分
(2)由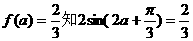
即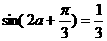 …………7分
…………7分
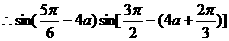
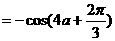 …………9分
…………9分
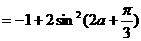 …………11分
…………11分
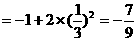 …………12分
…………12分
1.解:(1)记“甲取到黑球”为事件A,“乙取到黑球为事件B”
则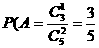 …………3分
…………3分
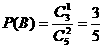 故甲、乙取到黑球的概率均为
故甲、乙取到黑球的概率均为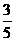 …………6分
…………6分
(2)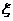 的所有可能取值为0,1,2
的所有可能取值为0,1,2
且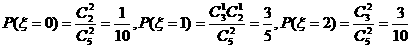
∴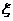 的分布列为
的分布列为
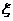 |
0 |
1 |
2 |
|
P |
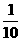 |
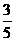 |
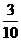 |
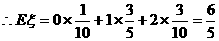
(注意:错误算法的答案也是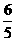 ) …………12分
) …………12分
12.(本题满分14分)w.w.^w.k.s.5*
已知函数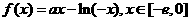 ,
,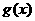 =
=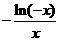 ,其中
,其中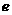 是自然对数的底数,
是自然对数的底数,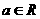 。
。
(1) 讨论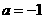 时
时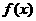 的单调性并求
的单调性并求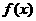 的最小值;
的最小值;
(2) 求证:在(1)的条件下,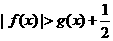 ;
;
(3) 是否存在实数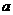 ,使
,使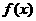 的最小值是3,如果村在,求出
的最小值是3,如果村在,求出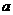 的值;如果不存在,请说明理由w.w.^w.k.s.5*
的值;如果不存在,请说明理由w.w.^w.k.s.5*
11.(本题满分12分)
已在数列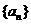 有
有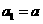 ,
,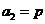 (常数
(常数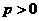 ),对任意的正整数
),对任意的正整数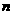 ,
,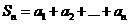 ,并有
,并有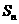 满足
满足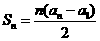 w.w.^w.k.s.5*
w.w.^w.k.s.5*
(1) 求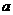 的值;
的值;
(2) 试判断数列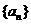 是否是等差数列,若是,求其通项公式,若不是,说明理由;
是否是等差数列,若是,求其通项公式,若不是,说明理由;
(3) 令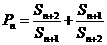 ,
,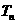 是数列
是数列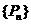 的前n项和,求证:
的前n项和,求证: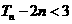
10.(本题满分12分)w.w.^w.k.s.5*
已知双曲线的中心在原点,离心率为2,一个焦点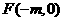 (m是正常数)
(m是正常数)
①求双曲线方程
②设Q是双曲线上一点,且过点F、Q的直线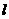 与
与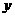 轴交于点M,若
轴交于点M,若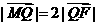 ,求直线
,求直线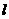 的方程。
的方程。
9.(本题满分12分)w.w.^w.k.s.5*
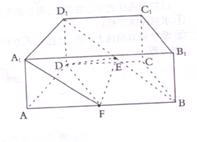 直四棱住
直四棱住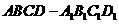 中,底面ABCD是等腰梯形
中,底面ABCD是等腰梯形
,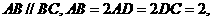 E为
E为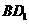 的中点,
的中点,
F为AB中点。
①求证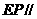 平面
平面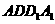 ;
;
②若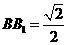 ,求
,求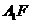 与平面
与平面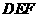 所成的大小。
所成的大小。
8.(本题满分12分)w.w.^w.k.s.5*
5个球分别标有数字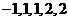 ,从中任取2个球,随机变量
,从中任取2个球,随机变量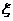 表示两球上所标数字之和。
表示两球上所标数字之和。
①求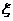 的概率分布;
的概率分布;
②求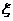 的数学期望
的数学期望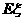 和方差
和方差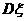 。
。
7.(本题满分12分)
已知三点: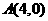 ,
,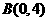 ,
,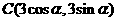
①若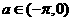 ,且
,且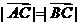 ,求角
,求角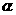 的值;
的值;
②若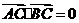 ,求
,求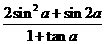 w.w.^w.k.s.5*
w.w.^w.k.s.5*
6.(本小题满分14分)
已知数列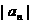 满足:
满足: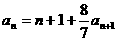 ,且存在大于1的整数k使
,且存在大于1的整数k使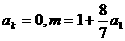 。
。
(1)用k表示m(化成最简形式);
(2)若m是正整数,求k与m的值;
(3)当k大于7时,试比较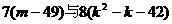 的大小。
的大小。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com