
题目列表(包括答案和解析)
1.能借助空间几何体内的位置关系求空间的夹角和距离;
2.向量在空间中的应用
在空间坐标系下,通过向量的坐标的表示,运用计算的方法研究三维空间几何图形的性质。
在复习过程中,抓住源于课本,高于课本的指导方针。本讲考题大多数是课本的变式题,即源于课本。因此,掌握双基、精通课本是本章关键
本讲内容主要有空间直角坐标系,空间向量的坐标表示,空间向量的坐标运算,平行向量,垂直向量坐标之间的关系以及中点公式.空间直角坐标系是选取空间任意一点O和一个单位正交基底{i,j,k}建立坐标系,对于O点的选取要既有作图的直观性,而且使各点的坐标,直线的坐标表示简化,要充分利用空间图形中已有的直线的关系和性质;空间向量的坐标运算同平面向量类似,具有类似的运算法则.一个向量在不同空间的表达方式不一样,实质没有改变.因而运算的方法和运算规律结论没变。如向量的数量积a·b=|a|·|b|cos<a,b>在二维、三维都是这样定义的,不同点仅是向量在不同空间具有不同表达形式.空间两向量平行时同平面两向量平行时表达式不一样,但实质是一致的,即对应坐标成比例,且比值为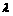 ,对于中点公式要熟记
,对于中点公式要熟记
对本讲内容的考查主要分以下三类:
1.以选择、填空题型考查本章的基本概念和性质
此类题一般难度不大,用以解决有关长度、夹角、垂直、判断多边形形状等问题。
6.. 已知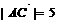 ,
,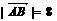 ,
,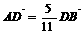 ,
,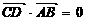 。
。
(1)求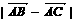 ;
;
(2)设∠BAC=θ,且已知cos(θ+x)=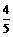 ,
,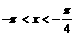 ,求sinx
,求sinx
解:(1)由已知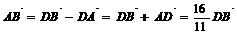
∴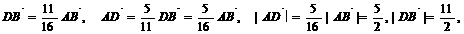
∵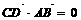 ∴CD⊥AB,在Rt△BCD中BC2=BD2+CD2,
∴CD⊥AB,在Rt△BCD中BC2=BD2+CD2,
又CD2=AC2-AD2, 所以BC2=BD2+AC2-AD2=49, ……4分
所以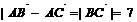 ……6分
……6分
(2)在△ABC中,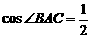 ∴
∴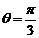 ……8分
……8分
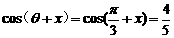
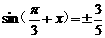
而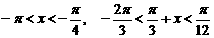 如果
如果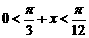 ,
,
则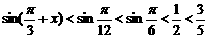 ∴
∴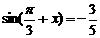 ……10分
……10分
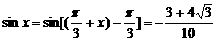
5.已知a=( ,
,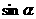 ),b=(
),b=(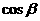 ,
,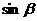 ),a与b之间有关系式|ka+b|=
),a与b之间有关系式|ka+b|=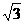 |a-kb|,其中k>0.
|a-kb|,其中k>0.
(1)用k表示a、b;
(2)求a·b的最小值,并求此时,a与b的夹角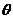 的大小.
的大小.
由已知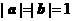 .
.
∵ 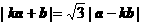 ,∴
,∴ 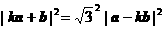 .∴
.∴ 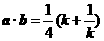 .
.
∵ k>0, ∴ 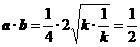 .
.
此时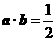 ∴
∴ 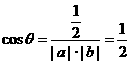 . ∴
. ∴ 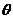 =60°.
=60°.
4、已知平面向量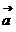 =(
=(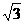 ,-1),
,-1),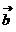 = (
= (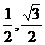 ).
).
(1)求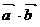 ;
;
(2)设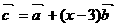 ,
,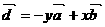 (其中
(其中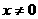 ),若
),若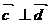 ,试求函数关系式
,试求函数关系式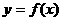 并解不等式
并解不等式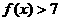 .(1)
.(1)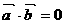 ;
;
(2)由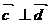 得,
得,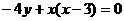 ,
,
所以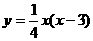 ;
;
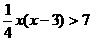 变形得:
变形得: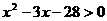 ,解得
,解得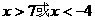 .
.
3.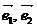 是平面内不共线两向量,已知
是平面内不共线两向量,已知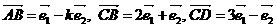 ,若
,若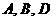 三点共线,则
三点共线,则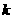 的值是
的值是
A.2 B.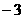 C.
C.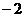 D.
D.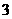
A 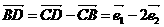 ,又A、B、D三点共线,则
,又A、B、D三点共线,则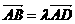 .即
.即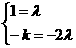 ,∴
,∴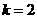 ,故选
,故选 .
.
[总结点评]本题主要考查共线向量的定义和平面向量基本定理的运用. 要求我们熟记公式,掌握常见变形技巧与方法.
2.如图,设P、Q为△ABC内的两点,且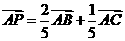 ,
,
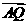 =
=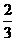
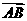 +
+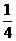
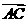 ,则△ABP的面积与△ABQ的面积之比为
,则△ABP的面积与△ABQ的面积之比为
A.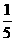 B.
B. 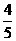 C.
C.
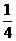 D.
D.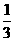
如下图,设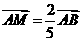 ,
,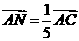 ,则
,则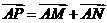 .
.
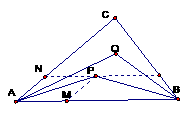 由平行四边形法则,知NP∥AB,所以
由平行四边形法则,知NP∥AB,所以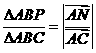 =
=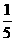 ,
,
同理可得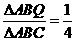 .故
.故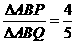 ,选B.
,选B.
题型1:空间向量的概念及性质
例1.有以下命题:①如果向量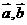 与任何向量不能构成空间向量的一组基底,那么
与任何向量不能构成空间向量的一组基底,那么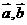 的关系是不共线;②
的关系是不共线;②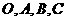 为空间四点,且向量
为空间四点,且向量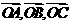 不构成空间的一个基底,那么点
不构成空间的一个基底,那么点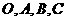 一定共面;③已知向量
一定共面;③已知向量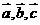 是空间的一个基底,则向量
是空间的一个基底,则向量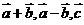 ,也是空间的一个基底。其中正确的命题是(
)
,也是空间的一个基底。其中正确的命题是(
)
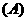 ①②
①② 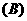 ①③
①③  ②③
②③ 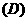 ①②③
①②③
解析:对于①“如果向量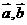 与任何向量不能构成空间向量的一组基底,那么
与任何向量不能构成空间向量的一组基底,那么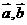 的关系一定共线”;所以①错误。②③正确。
的关系一定共线”;所以①错误。②③正确。
点评:该题通过给出命题的形式考察了空间向量能成为一组基的条件,为此我们要掌握好空间不共面与不共线的区别与联系
例2.下列命题正确的是( )
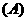 若
若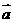 与
与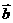 共线,
共线,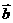 与
与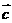 共线,则
共线,则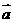 与
与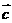 共线;
共线;
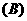 向量
向量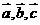 共面就是它们所在的直线共面;
共面就是它们所在的直线共面;
 零向量没有确定的方向;
零向量没有确定的方向;
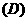 若
若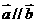 ,则存在唯一的实数
,则存在唯一的实数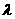 使得
使得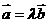 ;
;
解析:A中向量 为零向量时要注意,B中向量的共线、共面与直线的共线、共面不一样,D中需保证
为零向量时要注意,B中向量的共线、共面与直线的共线、共面不一样,D中需保证 不为零向量
不为零向量
答案C。
点评:零向量是一个特殊的向量,时刻想着零向量这一特殊情况对解决问题有很大用处。像零向量与任何向量共线等性质,要兼顾
题型2:空间向量的基本运算
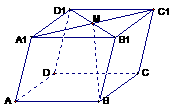 例3.如图:在平行六面体
例3.如图:在平行六面体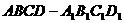 中,
中,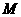 为
为 与
与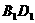 的交点。若
的交点。若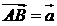 ,
,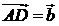 ,
,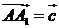 ,则下列向量中与
,则下列向量中与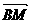 相等的向量是( )
相等的向量是( )
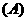
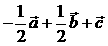
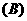
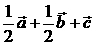

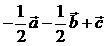
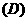
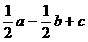
解析:显然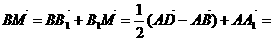
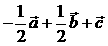 ;
;
答案为A。
点评:类比平面向量表达平面位置关系过程,掌握好空间向量的用途。用向量的方法处理立体几何问题,使复杂的线面空间关系代数化,本题考查的是基本的向量相等,与向量的加法.考查学生的空间想象能力
例4.已知: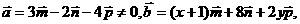 且
且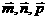 不共面.若
不共面.若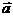 ∥
∥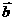 ,求
,求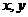 的值.
的值.
解:
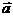 ∥
∥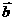 ,,且
,,且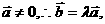 即
即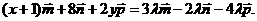
又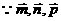 不共面,
不共面,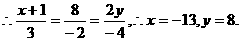
点评:空间向量在运算时,注意到如何实施空间向量共线定理。
题型3:空间向量的坐标
例5.(1)已知两个非零向量 =(a1,a2,a3),
=(a1,a2,a3), =(b1,b2,b3),它们平行的充要条件是( )
=(b1,b2,b3),它们平行的充要条件是( )
A.  :|
:| |=
|= :|
:| | B.a1·b1=a2·b2=a3·b3
| B.a1·b1=a2·b2=a3·b3
C.a1b1+a2b2+a3b3=0 D.存在非零实数k,使 =k
=k
(2)已知向量 =(2,4,x),
=(2,4,x), =(2,y,2),若|
=(2,y,2),若| |=6,
|=6, ⊥
⊥ ,则x+y的值是( )
,则x+y的值是( )
A. -3或1 B.3或-1 C. -3 D.1
(3)下列各组向量共面的是( )
A.  =(1,2,3),
=(1,2,3), =(3,0,2),
=(3,0,2),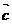 =(4,2,5)
=(4,2,5)
B.  =(1,0,0),
=(1,0,0), =(0,1,0),
=(0,1,0),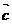 =(0,0,1)
=(0,0,1)
C.  =(1,1,0),
=(1,1,0), =(1,0,1),
=(1,0,1),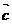 =(0,1,1)
=(0,1,1)
D.  =(1,1,1),
=(1,1,1), =(1,1,0),
=(1,1,0),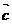 =(1,0,1)
=(1,0,1)
解析:(1)D;点拨:由共线向量定线易知;
(2)A 点拨:由题知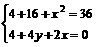

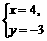 或
或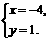 ;
;
(3)A 点拨:由共面向量基本定理可得
点评:空间向量的坐标运算除了数量积外就是考察共线、垂直时参数的取值情况
例6.已知空间三点A(-2,0,2),B(-1,1,2),C(-3,0,4)。设 =
=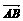 ,
, =
=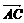 ,(1)求
,(1)求 和
和 的夹角
的夹角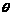 ;(2)若向量k
;(2)若向量k +
+ 与k
与k -2
-2 互相垂直,求k的值.
互相垂直,求k的值.
思维入门指导:本题考查向量夹角公式以及垂直条件的应用,套用公式即可得到所要求的结果.
解:∵A(-2,0,2),B(-1,1,2),C(-3,0,4), =
=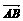 ,
, =
=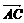 ,
,
∴ =(1,1,0),
=(1,1,0), =(-1,0,2).
=(-1,0,2).
(1)cos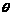 =
=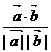 =
=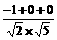
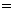 -
-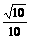 ,
,
∴ 和
和 的夹角为-
的夹角为-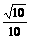 。
。
(2)∵k +
+ =k(1,1,0)+(-1,0,2)=(k-1,k,2),
=k(1,1,0)+(-1,0,2)=(k-1,k,2),
k -2
-2 =(k+2,k,-4),且(k
=(k+2,k,-4),且(k +
+ )⊥(k
)⊥(k -2
-2 ),
),
∴(k-1,k,2)·(k+2,k,-4)=(k-1)(k+2)+k2-8=2k2+k-10=0。
则k=-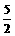 或k=2。
或k=2。
点拨:第(2)问在解答时也可以按运算律做。( +
+ )(k
)(k -2
-2 )=k2
)=k2 2-k
2-k ·
· -2
-2 2=2k2+k-10=0,解得k=-
2=2k2+k-10=0,解得k=-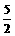 ,或k=2。
,或k=2。
题型4:数量积
例7(2009江西卷文)如图,在四面体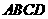 中,截面
中,截面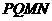 是正方形,则在下列命题中,错误的为
是正方形,则在下列命题中,错误的为
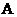 .
. 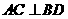
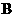 .
.  ∥截面
∥截面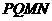
 .
. 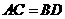
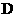 . 异面直线
. 异面直线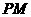 与
与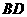 所成的角为
所成的角为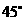
答案:C
[解析]由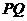 ∥
∥ ,
,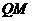 ∥
∥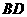 ,
,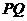 ⊥
⊥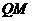 可得
可得 ⊥
⊥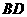 ,故
,故 正确;由
正确;由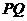 ∥
∥ 可得
可得 ∥截面
∥截面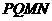 ,故
,故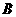 正确;
正确;
异面直线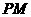 与
与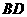 所成的角等于
所成的角等于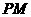 与
与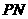 所成的角,故
所成的角,故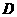 正确;
正确;
综上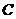 是错误的,故选
是错误的,故选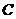 .
.
点评:本题考查平面向量的数量积及运算律
例8.(1)设向量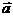 与
与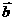 的夹角为
的夹角为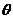 ,
,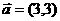 ,
,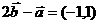 ,
,
则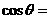 .
.
.解:设向量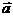 与
与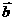 的夹角为
的夹角为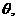 且
且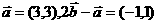 ∴
∴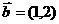 ,则
,则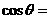
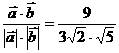 =
=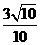 .
.
(2)设空间两个不同的单位向量 =(x1,y1,0),
=(x1,y1,0), =(x2,y2,0)与向量
=(x2,y2,0)与向量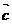 =(1,1,1)的夹角都等于
=(1,1,1)的夹角都等于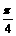 。(1)求x1+y1和x1y1的值;(2)求<
。(1)求x1+y1和x1y1的值;(2)求< ,
, >的大小(其中0<<
>的大小(其中0<< ,
, ><π
><π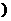 。
。
解析
(2)解:(1)∵| |=|
|=| |=1,∴x
|=1,∴x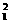 +y
+y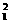 =1,∴x
=1,∴x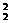 =y
=y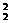 =1.
=1.
又∵ 与
与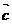 的夹角为
的夹角为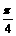 ,∴
,∴ ·
·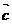 =|
=| ||
||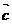 |cos
|cos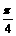 =
=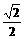
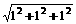 =
=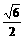 .
.
又∵ ·
·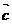 =x1+y1,∴x1+y1=
=x1+y1,∴x1+y1=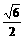 。
。
另外x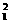 +y
+y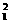 =(x1+y1)2-2x1y1=1,∴2x1y1=(
=(x1+y1)2-2x1y1=1,∴2x1y1=(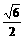 )2-1=
)2-1=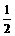 .∴x1y1=
.∴x1y1=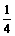 。
。
(2)cos< ,
, >=
>=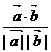 =x1x2+y1y2,由(1)知,x1+y1=
=x1x2+y1y2,由(1)知,x1+y1=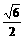 ,x1y1=
,x1y1=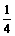 .∴x1,y1是方程x2-
.∴x1,y1是方程x2-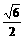 x+
x+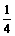 =0的解.
=0的解.
∴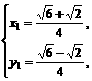 或
或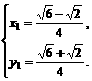 同理可得
同理可得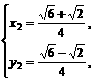 或
或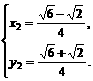
∵ ≠
≠ ,∴
,∴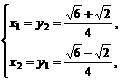 或
或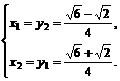
∴cos< ,
, >=
>=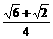 ·
·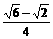 +
+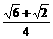 ·
·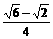 =
=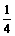 +
+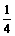 =
=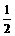 .
.
∵0≤< ,
, >≤π,∴<
>≤π,∴< ,
, >=
>=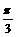 。
。
评述:本题考查向量数量积的运算法则
题型5:空间向量的应用
例9.(1)已知a、b、c为正数,且a+b+c=1,求证: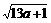 +
+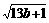 +
+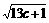 ≤4
≤4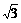 。
。
(2)已知F1=i+2j+3k,F2=-2i+3j-k,F3=3i-4j+5k,若F1,F2,F3共同作用于同一物体上,使物体从点M1(1,-2,1)移到点M2(3,1,2),求物体合力做的功。
解析:(1)设 =(
=(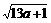 ,
,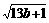 ,
,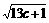 ),
),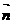 =(1,1,1),
=(1,1,1),
则| |=4,|
|=4,|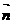 |=
|=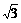 .
.
∵ ·
·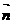 ≤|
≤| |·|
|·|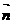 |,
|,
∴ ·
·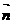 =
=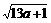 +
+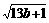 +
+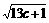 ≤|
≤| |·|
|·|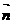 |=4
|=4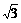 .
.
当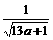 =
=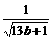 =
=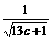 时,即a=b=c=
时,即a=b=c=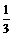 时,取“=”号。
时,取“=”号。
(2)解:W=F·s=(F1+F2+F3)·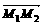 =14。
=14。
点评:若 =(x,y,z),
=(x,y,z),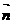 =(a,b,c),则由
=(a,b,c),则由 ·
·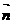 ≤|
≤| |·|
|·|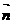 |,得(ax+by+cz)2≤(a2+b2+c2)(x2+y2+z2).此式又称为柯西不等式(n=3)。本题考查|
|,得(ax+by+cz)2≤(a2+b2+c2)(x2+y2+z2).此式又称为柯西不等式(n=3)。本题考查| |·|
|·| |≥
|≥ ·
· 的应用,解题时要先根据题设条件构造向量
的应用,解题时要先根据题设条件构造向量 ,
, ,然后结合数量积性质进行运算。空间向量的数量积对应做功问题
,然后结合数量积性质进行运算。空间向量的数量积对应做功问题
例10.如图,直三棱柱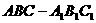 中,
中,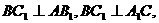 求证:
求证: 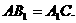
证明: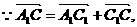
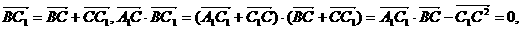
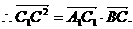
同理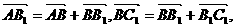
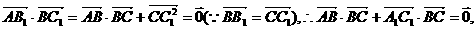
又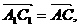
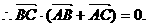
设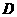 为
为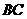 中点,则
中点,则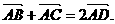
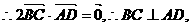
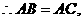 又
又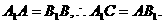
点评:从上述例子可以看出,利用空间向量来解决位置关系问题,要用到空间多边形法则,向量的运算,数量积以及平行,相等和垂直的条件
1.过△ABC的重心任作一直线分别交AB,AC于点D、E.若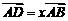 ,
,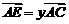 ,
,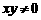 ,则
,则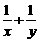 的值为( )
的值为( )
(A)4 (B)3 (C)2 (D)1
解析:取△ABC为正三角形易得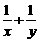 =3.选B.
=3.选B.
评析:本题考查向量的有关知识,如果按常规方法就比较难处理,但是用特殊值的思想就比较容易处理,考查学生灵活处理问题的能力.
6.数量积
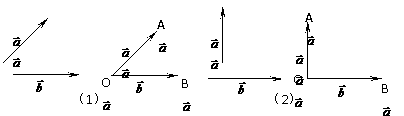
(1)夹角:已知两个非零向量 、
、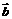 ,在空间任取一点O,作
,在空间任取一点O,作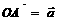 ,
,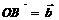 ,则角∠AOB叫做向量
,则角∠AOB叫做向量 与
与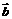 的夹角,记作
的夹角,记作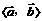
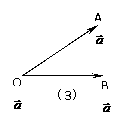 说明:⑴规定0≤
说明:⑴规定0≤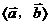 ≤
≤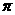 ,因而
,因而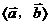 =
=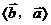 ;
;
⑵如果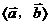 =
=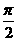 ,则称
,则称 与
与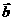 互相垂直,记作
互相垂直,记作 ⊥
⊥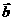 ;
;
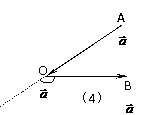 ⑶在表示两个向量的夹角时,要使有向线段的起点重合,注意图(3)、(4)中的两个向量的夹角不同,
⑶在表示两个向量的夹角时,要使有向线段的起点重合,注意图(3)、(4)中的两个向量的夹角不同,
图(3)中∠AOB=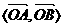 ,
,
图(4)中∠AOB=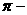
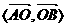 ,
,
从而有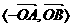 =
=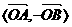 =
=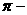
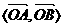 .
.
(2)向量的模:表示向量的有向线段的长度叫做向量的长度或模。
(3)向量的数量积: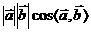 叫做向量
叫做向量 、
、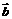 的数量积,记作
的数量积,记作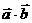 。
。
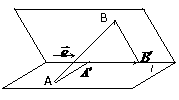 即
即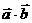 =
=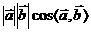 ,
,
向量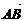
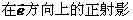 :
:
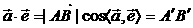
(4)性质与运算率

 ⑴
⑴ 。
⑴
。
⑴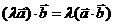
⑵ ⊥
⊥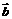

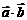 =0
⑵
=0
⑵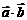 =
=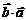
⑶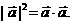 ⑶
⑶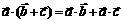
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com