
题目列表(包括答案和解析)
8.(2010广东文)

7.(2010广东理)16、(本小题满分14分)
已知函数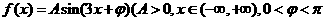 在
在 时取得最大值4.
时取得最大值4.
(1) 求 的最小正周期;
的最小正周期;
(2) 求 的解析式;
的解析式;
(3) 若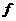 (
( α +
α +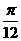 )=
)=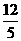 ,求sinα.
,求sinα.

 ,
, ,
,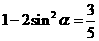 ,
,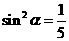 ,
, .
.
6.(2010北京理)(15)(本小题共13分)
已知函数
 。
。
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的最大值和最小值。
的最大值和最小值。
解:(I)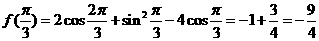
(II)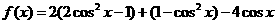
=
= ,
,
因为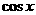

 ,
,
所以,当 时,
时, 取最大值6;当
取最大值6;当 时,
时, 取最小值
取最小值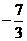
5.(2010北京文)(15)(本小题共13分)
已知函数
(Ⅰ)求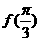 的值;
的值;
(Ⅱ)求 的最大值和最小值
的最大值和最小值
解:(Ⅰ)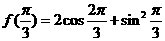 =
=
(Ⅱ)

因为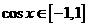 ,所以,当
,所以,当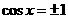 时
时 取最大值2;当
取最大值2;当 时,
时, 去最小值-1。
去最小值-1。
4.(2010浙江文)(18)(本题满分)在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足 。
。
(Ⅰ)求角C的大小;
(Ⅱ)求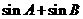 的最大值。
的最大值。

3.(2010江西理)17.(本小题满分12分)
已知函数 。
。
(1) 当m=0时,求 在区间
在区间 上的取值范围;
上的取值范围;
(2) 当 时,
时,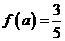 ,求m的值。
,求m的值。
[解析]考查三角函数的化简、三角函数的图像和性质、已知三角函数值求值问题。依托三角函数化简,考查函数值域,作为基本的知识交汇问题,考查基本三角函数变换,属于中等题.
解:(1)当m=0时,
 ,由已知
,由已知 ,得
,得
从而得: 的值域为
的值域为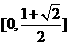
(2)
化简得:
当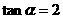 ,得:
,得: ,
,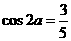 ,
,
代入上式,m=-2.
2.(2010浙江理)(18)(本题满分l4分)在△ABC中,角A、B、C所对的边分别为a,b,c,已知
(I)求sinC的值;
(Ⅱ)当a=2, 2sinA=sinC时,求b及c的长.
解析:本题主要考察三角变换、正弦定理、余弦定理等基础知识,同事考查运算求解能力。
(Ⅰ)解:因为cos2C=1-2sin2C= ,及0<C<π
,及0<C<π
所以sinC=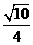 .
.
(Ⅱ)解:当a=2,2sinA=sinC时,由正弦定理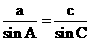 ,得
,得
c=4
由cos2C=2cos2C-1= ,J及0<C<π得
,J及0<C<π得
cosC=±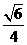
由余弦定理c2=a2+b2-2abcosC,得
b2±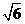 b-12=0
b-12=0
解得 b=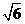 或2
或2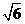

 所以 b=
所以 b=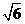 b=
b=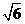
c=4 或 c=4
1.(2010湖南文)16. (本小题满分12分)
已知函数
(I)求函数 的最小正周期。
的最小正周期。
(II) 求函数 的最大值及
的最大值及 取最大值时x的集合。
取最大值时x的集合。

6.(2010江苏卷)10、定义在区间 上的函数y=6cosx的图像与y=5tanx的图像的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图像交于点P2,则线段P1P2的长为____________。
上的函数y=6cosx的图像与y=5tanx的图像的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图像交于点P2,则线段P1P2的长为____________。
解析 考查三角函数的图象、数形结合思想。线段P1P2的长即为sinx的值,
且其中的x满足6cosx=5tanx,解得sinx= 。线段P1P2的长为
。线段P1P2的长为
5.(2010福建理)14.已知函数 和
和 的图象的对称轴完全相同。若
的图象的对称轴完全相同。若 ,则
,则 的取值范围是
。
的取值范围是
。
[答案]
[解析]由题意知,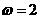 ,因为
,因为 ,所以
,所以 ,由三角函数图象知:
,由三角函数图象知:
 的最小值为
的最小值为 ,最大值为
,最大值为 ,所以
,所以 的取值范围是
的取值范围是 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com