
题目列表(包括答案和解析)
45.(2009北京理)若函数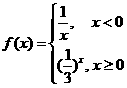 则不等式
则不等式 的解集为____________.
的解集为____________.
答案

解析 本题主要考查分段函数和简单绝对值不等式的解法. 属于基础知识、基本运算
的考查.
(1)由 .
.
(2)由 .
.
∴不等式 的解集为
的解集为 ,∴应填
,∴应填 .
.
41.(2009重庆卷理)若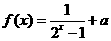 是奇函数,则
是奇函数,则 .
.
答案 
解析 解法1

42(2009上海卷文) 函数f(x)=x3+1的反函数f-1(x)=_____________.
答案 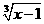
解析 由y=x3+1,得x= ,将y改成x,x改成y可得答案。
,将y改成x,x改成y可得答案。
44(2009北京文)已知函数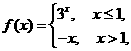 若
若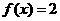 ,则
,则 .
.
.w.w.k.s.5 答案 
.w 解析 5.u.c本题主要考查分段函数和简单的已知函数值求 的值. 属于基础知识、基本运算的考查.
的值. 属于基础知识、基本运算的考查.
由 ,
, 无解,故应填
无解,故应填 .
.
40.(2009重庆卷文)把函数 的图像
的图像 向右平移
向右平移 个单位长度,再向下平移
个单位长度,再向下平移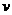 个单位长度后得到图像
个单位长度后得到图像 .若对任意的
.若对任意的 ,曲线
,曲线 与
与 至多只有一个交点,则
至多只有一个交点,则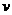 的最小值为 ( )
的最小值为 ( )
A.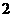 B.
B.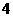 C.
C. D.
D.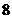
答案 B
解析 根据题意曲线C的解析式为 则方程
则方程
 ,即
,即 ,即
,即 对任意
对任意
 恒成立,于是
恒成立,于是 的最大值,令
的最大值,令 则
则

 由此知函数
由此知函数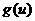 在(0,2)上为增函数,在
在(0,2)上为增函数,在 上为减函数,所以当
上为减函数,所以当 时,函数
时,函数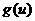 取最大值,即为4,于是
取最大值,即为4,于是 。
。
39. (2009福建卷文)定义在R上的偶函数
(2009福建卷文)定义在R上的偶函数 的部分图像如右图所示,则在
的部分图像如右图所示,则在 上,下列函数中与
上,下列函数中与 的单调性不同的是 ( )
的单调性不同的是 ( )
A.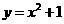
B. 
C. 
D.
答案 C
解析 解析
根据偶函数在关于原点对称的区间上单调性相反,故可知求在 上单调递减,注意到要与
上单调递减,注意到要与 的单调性不同,故所求的函数在
的单调性不同,故所求的函数在 上应单调递增。而函数
上应单调递增。而函数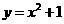 在
在 上递减;函数
上递减;函数 在
在 时单调递减;函数
时单调递减;函数
 在(
在( 上单调递减,理由如下y’=3x2>0(x<0),故函数单调递增, 显然符合题意;而函数
上单调递减,理由如下y’=3x2>0(x<0),故函数单调递增, 显然符合题意;而函数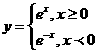 ,有y’=-
,有y’=-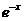 <0(x<0),故其在(
<0(x<0),故其在( 上单调递减, 不符合题意,综上选C。
上单调递减, 不符合题意,综上选C。
38.(2009福建卷文)下列函数中,与函数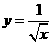 有相同定义域的是 ( )
有相同定义域的是 ( )
A .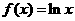 B.
B.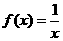 C.
C.  D.
D.
答案 A
解析 解析 由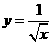 可得定义域是
可得定义域是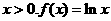 的定义域
的定义域 ;
;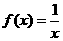 的定义域是
的定义域是 ≠0;
≠0; 的定义域是
的定义域是 定义域是
定义域是 。故选A.
。故选A.
37.(2009四川卷理)已知函数 是定义在实数集
是定义在实数集 上的不恒为零的偶函数,且对任意实数
上的不恒为零的偶函数,且对任意实数 都有
都有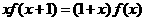 ,则
,则 的值是 (
)
的值是 (
)
A.0 B. C.1
D.
C.1
D.
[考点定位]本小题考查求抽象函数的函数值之赋值法,综合题。(同文12)
答案 A
解析 令 ,则
,则 ;令
;令 ,则
,则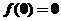
由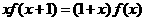 得
得 ,所以
,所以
 ,故选择A。
,故选择A。
36.(2009天津卷理)已知函数 若
若 则实数
则实数
的取值范围是 ( )
A  B
B  C
C  D
D 
[考点定位]本小题考查分段函数的单调性问题的运用。以及一元二次不等式的求解。
解析:由题知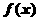 在
在 上是增函数,由题得
上是增函数,由题得 ,解得
,解得 ,故选择C。
,故选择C。
35.(2009湖南卷理)设函数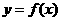 在(
在(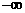 ,+
,+ )内有定义。对于给定的正数K,定义函数 ( )
)内有定义。对于给定的正数K,定义函数 ( )

取函数 =
= 。若对任意的
。若对任意的 ,恒有
,恒有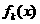 =
= ,则 (
)
,则 (
)
A.K的最大值为2 B. K的最小值为2
C.K的最大值为1 D. K的最小值为1
答案 D
解析 由 知
知 ,所以
,所以 时,
时, ,当
,当 时,
时, ,所以
,所以 即
即 的值域是
的值域是 ,而要使
,而要使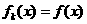 在
在 上恒成立,结合条件分别取不同的
上恒成立,结合条件分别取不同的 值,可得D符合,此时
值,可得D符合,此时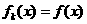 。故选D项。
。故选D项。
34.(2009湖南卷理)如图1,当参数 时,连续函数
时,连续函数 的图像分别对应曲线
的图像分别对应曲线 和
和 , 则
( )
, 则
( )
 A
A 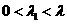 B
B

C  D
D

答案 B
解析 解析由条件中的函数是分式无理型函数,先由函
数在 是连续的,可知参数
是连续的,可知参数 ,即排除C,D项,又取
,即排除C,D项,又取 ,知对应函数值
,知对应函数值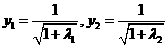 ,由图可知
,由图可知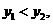 所以
所以 ,即选B项。
,即选B项。
33.(2009湖北卷文)函数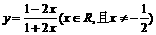 的反函数是 ( )
的反函数是 ( )
A. B.
B.
C. D.
D.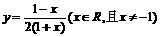
答案 D
解析 可反解得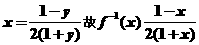 且可得原函数中y∈R、y≠-1所以
且可得原函数中y∈R、y≠-1所以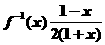 且x∈R、x≠-1选D
且x∈R、x≠-1选D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com